Понятие предела числовой последовательности
Вспомним сначала определение числовой последовательности.
Определение 1
Отображения множества натуральных чисел на множество действительных чисел называется числовой последовательностью .
Понятие предела числовой последовательности имеет несколько основных определений:
- Действительное число $a$ называется пределом числовой последовательности $(x_n)$, если для любого $\varepsilon >0$ существует номер $N$, зависящий от $\varepsilon$, такой, что для любого номера $n> N$ выполняется неравенство $\left|x_n-a\right|
- Действительное число $a$ называется пределом числовой последовательности $(x_n)$, если в любую окрестность точки $a$ попадают все члены последовательности $(x_n)$, за исключением, быть может, конечного числа членов.
Рассмотрим пример вычисления значения предела числовой последовательности:
Пример 1
Найти предел ${\mathop{lim}_{n\to \infty } \frac{n^2-3n+2}{2n^2-n-1}\ }$
Решение:
Для решения данного задания вначале нам необходимо вынести за скобки старшую степень, входящую в выражение:
${\mathop{lim}_{n\to \infty } \frac{n^2-3n+2}{2n^2-n-1}\ }={\mathop{lim}_{x\to \infty } \frac{n^2\left(1-\frac{3}{n}+\frac{2}{n^2}\right)}{n^2\left(2-\frac{1}{n}-\frac{1}{n^2}\right)}\ }={\mathop{lim}_{n\to \infty } \frac{1-\frac{3}{n}+\frac{2}{n^2}}{2-\frac{1}{n}-\frac{1}{n^2}}\ }$
Если в знаменателе стоит бесконечно большая величина, то весь предел стремится к нулю, $\mathop{lim}_{n\to \infty }\frac{1}{n}=0$, использовав это, получим:
${\mathop{lim}_{n\to \infty } \frac{1-\frac{3}{n}+\frac{2}{n^2}}{2-\frac{1}{n}-\frac{1}{n^2}}\ }=\frac{1-0+0}{2-0-0}=\frac{1}{2}$
Ответ: $\frac{1}{2}$.
Понятие предела функции в точке
Понятие предела функции в точке имеет два классических определения:
Определение термина «предел» по Коши
Действительное число $A$ называется пределом функции $f\left(x\right)$ при $x\to a$, если для любого $\varepsilon > 0$ существует $\delta >0$, зависящий от $\varepsilon $, такой, что для любого $x\in X^{\backslash a}$, удовлетворяющих неравенству $\left|x-a\right|
Определение по Гейне
Действительное число $A$ называется пределом функции $f\left(x\right)$ при $x\to a$, если для любой последовательности $(x_n)\in X$, сходящейся к числу $a$, последовательность значений $f(x_n)$ сходится к числу $A$.
Эти два определения связаны между собой.
Замечание 1
Определения предела функции по Коши и по Гейне эквивалентны.
Помимо классических подходов к вычислению пределов функции, вспомним формулы, которые могут также помочь в этом.
Таблица эквивалентных функций, когда $x$ бесконечно мал (стремится к нулю)
Одним из подходов к решению пределов является принцип замены на эквивалентную функцию . Таблица эквивалентных функций представлена ниже, чтобы ей воспользоваться, необходимо вместо функций справа подставить в выражение соответствующую элементарную функцию слева.
Рисунок 1. Таблица эквивалентности функций. Автор24 - интернет-биржа студенческих работ
Также для решения пределов, значения которых сводятся к неопределённости, возможно применить правило Лопиталя. В общем случае неопределённость вида $\frac{0}{0}$ можно раскрыть разложив на множители числитель и знаменатель и затем сократив. Неопределённость, имеющую форму $\frac{\infty }{\infty}$ возможно разрешить после деления выражений в числителе и знаментателе на переменную, при которой находится старшая степень.
Замечательные пределы
- Первый замечательный предел:
${\mathop{lim}_{x\to 0} \frac{sinx}{x}\ }=1$
- Второй замечательный предел:
$\mathop{lim}_{x\to 0}{(1+x)}^{\frac{1}{x}}=e$
Специальные пределы
- Первый специальный предел:
$\mathop{lim}_{x\to 0}\frac{{{log}_a (1+x-)\ }}{x}={{log}_a e\ }=\frac{1}{lna}$
- Второй специальный предел:
$\mathop{lim}_{x\to 0}\frac{a^x-1}{x}=lna$
- Третий специальный предел:
$\mathop{lim}_{x\to 0}\frac{{(1+x)}^{\mu }-1}{x}=\mu $
Непрерывность функции
Определение 2
Функция $f(x)$ называется непрерывной в точке $x=x_0$, если $\forall \varepsilon >{\rm 0}$ $\exists \delta (\varepsilon ,E_{0})>{\rm 0}$ такое, что $\left|f(x)-f(x_{0})\right|
Функция $f(x)$ непрерывна в точке $х=х_0$, если $\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm x}_{{\rm 0}} } f(x)=f(x_{0})$.
Точка $x_0\in X$ называется точкой разрыва первого рода, если в ней существуют конечные пределы ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, но нарушается равенство ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }=f(x_0)$
Причем, если ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }\ne f(x_0)$, то это точка устранимого разрыва, а если ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }\ne {\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, то точка скачка функции.
Точка $x_0\in X$ называется точкой разрыва второго рода, если в ней хотя бы один из пределов ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$ представляет собой бесконечность или не существует.
Пример 2
Исследовать на непрерывность $y=\frac{2}{x}$
Решение:
${\mathop{lim}_{x\to 0-0} f(x)\ }={\mathop{lim}_{x\to 0-0} \frac{2}{x}\ }=-\infty $ - функция имеет точку разрыва второго рода.
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ
В результате измерения физических величин (время, площадь, объем, масса, скорость и т.д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь от их конкретного содержания. В дальнейшем, говоря о величинах, мы будем иметь в виду их числовые значения. В различных явлениях некоторые величины изменяются, а другие сохраняют свое числовое значение. Например, при равномерном движении точки время и расстояние меняются, а скорость остается постоянной.
Переменной величиной называется величина, которая принимает различные числовые значения. Величина, числовые значения которой не меняются, называется постоянной . Переменные величины будем обозначать буквами x, y, z,… , постоянные – a, b, c,…
Заметим, что в математике постоянная величина часто рассматривается как частный случай переменной, у которой все числовые значения одинаковы.
Областью изменения переменной величины называется совокупность всех принимаемых ею числовых значений. Область изменения может состоять как из одного или нескольких промежутков, так и из одной точки.
УПОРЯДОЧЕННАЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Будем говорить, что переменная x есть упорядоченная переменная величина , если известна область ее изменения, и про каждые из двух любых ее значений можно сказать, какое из них предыдущее и какое последующее.
Частным случаем упорядоченной переменной величины является переменная величина, значения которой образуют числовую последовательность x 1 ,x 2 ,…,x n ,… Для таких величин при i < j, i, j Î N , значение x i считается предшествующим, а x j – последующим независимо от того, какое из этих значений больше. Таким образом, числовая последовательность – это переменная величина, последовательные значения которой могут быть перенумерованы. Числовую последовательность будем обозначать . Отдельные числа последовательности называются ее элементами .
Например, числовую последовательность образуют следующие величины:
ФУНКЦИЯ
При изучении различных явлений природы и решении технических задач, а, следовательно, и в математике приходится рассматривать изменение одной величины в зависимости от изменения другой. Так, например, известно, что площадь круга выражается через радиус формулой S = πr 2 . Если радиус r принимает различные числовые значения, то площадь S также принимает различные числовые значения, т.е. изменение одной переменной влечет изменение другой.
Если каждому значению переменной x , принадлежащему некоторой области, соответствует одно определенное значение другой переменной y , то y называется функцией переменной х . Символически будем записывать y=f(x) . При этом переменная x называется независимой переменной или аргументом .
Запись y=C , где C – постоянная, обозначает функцию, значение которой при любом значении x одно и то же и равно C .
Множество значений x , для которых можно определить значения функции y по правилу f(x) , называется областью определения функции .
Заметим, что числовая последовательность также является функцией, область определения которой совпадает с множеством натуральных чисел.
К основным элементарным функциям относятся все функции, изучаемые в школьном курсе математики:
Элементарной функцией называется функция, которая может быть задана основными элементарными функциями и постоянными при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
ПОНЯТИЕ ПРЕДЕЛА ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
В дальнейшем курсе математики понятие предела будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа – производная, интеграл и др.
Начнем с понятия предела числовой последовательности.
Число a называется пределом последовательности x = {x n }, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N , что при всех n>N выполняется неравенство |x n - a| < ε.
Если число a есть предел последовательности x = {x n }, то говорят, что x n стремится к a , и пишут .
Чтобы сформулировать это определение в геометрических терминах введем следующее понятие.
Окрестностью точки x 0 называется произвольный интервал (a, b ), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x 0 , для которой x 0 является серединой, тогда x 0 называется центром окрестности, а величина (b –a )/2 – радиусом окрестности.
Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде
Это неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).
Следовательно, постоянное число a есть предел числовой последовательности {x n }, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a ) найдется такой элемент последовательности с номером N , что все последующие элементыс номерами n>N будут находиться внутри этой окрестности.
Примеры.
Сделаем несколько замечаний.
Замечание 1. Очевидно, что если все элементы числовой последовательности принимают одно и то же постоянное значение x n = c , то предел этой последовательности будет равен самой постоянной. Действительно, при любом ε всегда выполняется неравенство |x n - c | = |c - c | = 0 < ε.
Замечание 2. Из определения предела следует, что последовательность не может иметь двух пределов. Действительно, предположим, что x n → a и одновременно x n → b . Возьмем любое и отметим окрестности точек a и b радиуса ε (см. рис.). Тогда по определению предела, все элементы последовательности, начиная с некоторого, должны находиться как в окрестности точки а , так и в окрестности точки b , что невозможно.
Замечание 3.
Не следует думать, что
каждая числовая последовательность имеет предел. Пусть, например, переменная
величина принимает значения 
. Несложно заметить, что эта последовательность не стремится
ни к какому пределу.
ПРЕДЕЛ ФУНКЦИИ
Пусть функция y=f(x) определена в некоторой окрестности точки a . Предположим, что независимая переменная x неограниченно приближается к числу a . Это означает, что мы можем придавать х значения сколь угодно близкие к a , но не равные a . Будем обозначать это так x → a . Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b .Тогда говорят, что число b есть предел функции f(x) при x → a .
Введем строгое определение предела функции.
Функция y=f(x) стремится к пределу b при x → a , если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x - a | < δ, имеет место неравенство |f(x) - b | < ε. Если b есть предел функции f(x) при x → a , то пишут или f(x) → b при x → a .
Проиллюстрируем это определение на графике функции. Т.к. из неравенства |x - a | < δ должно следовать неравенство |f(x) - b | < ε, т.е. при x Î (a - δ, a + δ) соответствующие значения функции f(x) Î (b - ε, b + ε), то, взяв произвольное ε > 0, мы можем подобрать такое число δ, что для всех точек x , лежащих в δ – окрестности точки a , соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y = b – ε и y = b + ε.
Несложно заметить, что предел функции должен обладать теми же свойствами, что и предел числовой последовательности, а именно и если при x → a функция имеет предел, то он единственный.
Примеры.
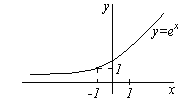
ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ В БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКЕ
До сих пор мы рассматривали пределы для случая, когда переменная величина x стремилась к определенному постоянному числу.
Будем говорить, что переменная x стремится к бесконечности , если для каждого заранее заданного положительного числа M (оно может быть сколь угодно большим) можно указать такое значение х=х 0 , начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x|>M .
Например, пусть переменная х принимает значения x 1 = –1, x 2 = 2, x 3 = –3, …, x n =(–1) n n, … Ясно, что это бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M .
Переменная величина x → +∞ , если при произвольном M > 0 все последующие значения переменной, начиная с некоторого, удовлетворяют неравенству x > M .
Аналогично, x → – ∞, если при любом M > 0 x < -M .
Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M , что для всех значений x , удовлетворяющих неравенству |x|>M , выполняется неравенство |f(x) - b | < ε.
Обозначают .
Примеры.
БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
Ранее мы рассмотрели случаи, когда функция f(x) стремилась к некоторому конечному пределу b при x → a или x → ∞.
Рассмотрим теперь случай, когда функция y=f(x) некотором способе изменения аргумента.
Функция f(x) стремится к бесконечности при x → a , т.е. является бесконечно большой величиной, если для любого числа М , как бы велико оно ни было, можно найти такое δ > 0, что для всех значений х ≠a , удовлетворяющих условию |x-a | < δ, имеет место неравенство |f(x) | > M .
Если f(x) стремится к бесконечности при x→a , то пишут или f(x) →∞ при x→a .
Сформулируйте аналогичное определение для случая, когда x →∞.
Если f(x) стремится к бесконечности при x→a и при этом принимает только положительные или только отрицательные значения, соответственно пишут или .
Примеры.
ОГРАНИЧЕННЫЕ ФУНКЦИИ
Пусть задана функция y=f(x) , определенная на некотором множестве D значений аргумента.
Функция y=f(x) называется ограниченной на множестве D , если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M . Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D .
Примеры.
- Функция y =sin x , определенная при -∞<x <+∞, является ограниченной, так как при всех значениях x |sin x |≤1 = M .
- Функция y =x 2 +2 ограничена, например, на отрезке , так как при всех x из этого отрезка |f(x)| ≤f (3) = 11.
- Рассмотрим функцию y =ln x при x Î (0; 1). Эта функция неограниченна на указанном отрезке, так как при x →0 ln x →-∞.
Функция y=f(x) называется ограниченной при x → a , если существует окрестность с центром в точке а , в которой функция ограничена.
Функция y=f(x) называется ограниченной при x→∞ , если найдется такое число N> 0, что при всех значениях х |x|>N , функция f(x) ограничена.
Установим связь между ограниченной функцией и функцией, имеющей предел.
Теорема 1. Если и b – конечное число, то функция f(x) ограничена при x→a .
Доказательство
. Т.к. , то при любом ε>0 найдется
такое число δ>0, что при вех значениях х
,
удовлетворяющих неравенству |x-a|<
δ, выполняется неравенство |f(x) –b|<
ε. Воспользовавшись свойством модуля |f(x) – b|≥|f(x)| - |b|
, последнее неравенство
запишем в виде |f(x)|<|b|+
ε. Таким образом, если
положить M=|b|+
ε, то при x→a |f(x)|
Замечание. Из определения ограниченной функции следует, что если , то она является неограниченной. Однако обратное неверно: неограниченная функция может не быть бесконечно большой. Приведите пример.
Теорема 2. Если , то функция y=1/f(x) ограничена при x→a .
Доказательство
. Из условия теоремы следует,
что при произвольном ε>0
в некоторой окрестности точки a
имеем |f(x) – b|<
ε. Т.к. |f(x) – b|=|b – f(x)| ≥|b| - |f(x)|
,
то |b| - |f(x)|<
ε. Следовательно, |f(x)|>|b| -
ε >0. Поэтому и 
Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø .
Квантор существования
∃- квантор существования , используется вместо слов "существует",
"имеется". Используется также сочетание символов ∃!, которое читается как существует единственный.
Абсолютная величина
Определение. Абсолютной величиной (модулем) действительного числа называется неотрицательное число , которое определяется по формуле:
Так, например,
Свойства модуля
Если и – действительные числа, то справедливы равенства:
Функция
зависимость между двумя или большим количеством величин, при которой каждым значениям одних величин, называемых аргументами функции, ставятся в соответствие значения других величин, называемых значениями функции.
Область определения функции
Областью определения функции называют те значения независимой переменной x, при которых все операции, входящие в функцию будут выполнимы.
Непрерывная функция
Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если
 |
Числовые последовательности
функция вида y = f (x ), x О N ,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f (n )или y 1 , y 2 ,…, y n ,…. Значения y 1 , y 2 , y 3 ,…называют соответственно первым, вторым, третьим, … членами последовательности.
Предел функции непрерывного аргумента
Число А называется пределом функции y=f(x) при x->x0,если для всех значений x, достаточно мало отличающихся от числа x0, соответствующие значения функции f(x) как угодно мало отличается от числа A
Бесконечно малая функция
Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
 |
Непрерывность функции. Точки разрыва.
Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!
На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность . Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.
Что нужно знать и уметь? Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции . Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций . Также желательно ознакомиться с геометрическими преобразованиями графиков , поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!
Непрерывность функции. Точки разрыва и их классификация
Понятие непрерывности функции
Рассмотрим некоторую функцию , непрерывную на всей числовой прямой:
Или, говоря лаконичнее, наша функция непрерывна на (множестве действительных чисел).
Каков «обывательский» критерий непрерывности? Очевидно, что график непрерывной функции можно начертить, не отрывая карандаша от бумаги.
При этом следует чётко отличать два простых понятия: область определения функции
и непрерывность функции
. В общем случае это не одно и то же
. Например:
Данная функция определена на всей числовой прямой, то есть для каждого
значения «икс» существует своё значение «игрека» . В частности, если , то . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное
значение функции. Таким образом, область определения
нашей функции: .
Однако эта функция не является непрерывной на ! Совершенно очевидно, что в точке она терпит разрыв . Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги. Немного позже мы рассмотрим классификацию точек разрыва.
Непрерывность функции в точке и на интервале
В той или иной математической задаче речь может идти о непрерывности функции в точке, непрерывности функции на интервале, полуинтервале или непрерывности функции на отрезке. То есть, не существует «просто непрерывности» – функция может быть непрерывной ГДЕ-ТО. И основополагающим «кирпичиком» всего остального является непрерывность функции в точке .
Теория математического анализа даёт определение непрерывности функции в точке с помощью «дельта» и «эпсилон» окрестностей, но на практике в ходу другое определение, которому мы и уделим самое пристальное внимание.
Сначала вспомним односторонние пределы
, ворвавшиеся в нашу жизнь на первом уроке о графиках функций
. Рассмотрим будничную ситуацию:
Если приближаться по оси к точке слева
(красная стрелка), то соответствующие значения «игреков» будут идти по оси к точке (малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела
:
Обратите внимание на запись (читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует , по сути это и обозначает, что мы подходим к числу с левой стороны.
Аналогично, если приближаться к точке «ка» справа
(синяя стрелка), то «игреки» придут к тому же значению , но уже по зелёной стрелке, и правосторонний предел
оформится следующим образом:
«Добавка» символизирует , и запись читается так: «икс стремится к ка справа».
Если односторонние пределы конечны и равны
(как в нашем случае): 
, то будем говорить, что существует ОБЩИЙ предел . Всё просто, общий предел – это наш «обычный» предел функции
, равный конечному числу.
Заметьте, что если функция не определена при (выколите чёрную точку на ветке графика), то перечисленные выкладки остаются справедливыми. Как уже неоднократно отмечалось, в частности, в статье о бесконечно малых функциях , выражения означают, что «икс» бесконечно близко приближается к точке , при этом НЕ ИМЕЕТ ЗНАЧЕНИЯ , определена ли сама функция в данной точке или нет. Хороший пример встретится в следующем параграфе, когда анализу подвергнется функция .
Определение : функция непрерывна в точке , если предел функции в данной точке равен значению функции в этой точке: .
Определение детализируется в следующих условиях:
1) Функция должна быть определена в точке , то есть должно существовать значение .
2) Должен существовать общий предел функции . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: 
.
3) Предел функции в данной точке должен быть равен значению функции в этой точке: .
Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке .
Непрерывность функции на интервале формулируется остроумно и очень просто: функция непрерывна на интервале , если она непрерывна в каждой точке данного интервала.
В частности, многие функции непрерывны на бесконечном интервале , то есть на множестве действительных чисел . Это линейная функция, многочлены, экспонента, синус, косинус и др. И вообще, любая элементарная функция непрерывна на своей области определения , так, например, логарифмическая функция непрерывна на интервале . Надеюсь, к данному моменту вы достаточно хорошо представляете, как выглядят графики основных функций. Более подробную информацию об их непрерывности можно почерпнуть у доброго человека по фамилии Фихтенгольц.
С непрерывностью функции на отрезке и полуинтервалах тоже всё несложно, но об этом уместнее рассказать на уроке о нахождении минимального и максимального значений функции на отрезке , а пока голову забивать не будем.
Классификация точек разрыва
Увлекательная жизнь функций богата всякими особенными точками, и точки разрыва лишь одна из страничек их биографии.
Примечание : на всякий случай остановлюсь на элементарном моменте: точка разрыва – это всегда отдельно взятая точка – не бывает «несколько точек разрыва подряд», то есть, нет такого понятия, как «интервал разрывов».
Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода . У каждого типа разрыва есть свои характерные особенности, которые мы рассмотрим прямо сейчас:
Точка разрыва первого рода
Если в точке нарушено условие непрерывности и односторонние пределы конечны , то она называется точкой разрыва первого рода .
Начнём с самого оптимистичного случая. По первоначальной задумке урока я хотел рассказать теорию «в общем виде», но чтобы продемонстрировать реальность материала, остановился на варианте с конкретными действующими лицами.
Уныло, как фото молодожёнов на фоне Вечного огня, но нижеследующий кадр общепринят. Изобразим на чертеже график функции :
Данная функция непрерывна на всей числовой прямой, кроме точки . И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко
приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
(Условие №2 непрерывности выполнено).
Но функция не определена в точке , следовательно, нарушено Условие №1 непрерывности, и функция терпит разрыв в данной точке.
Разрыв такого вида (с существующим общим пределом
) называют устранимым разрывом
. Почему устранимым? Потому что функцию можно доопределить
в точке разрыва:
Странно выглядит? Возможно. Но такая запись функции ничему не противоречит! Теперь разрыв устранён и все счастливы:
Выполним формальную проверку:
2) 
– общий предел существует;
3)
Таким образом, все три условия выполнены, и функция непрерывна в точке по определению непрерывности функции в точке.
Впрочем, ненавистники матана могут доопределить функцию нехорошим способом, например 
:
Любопытно, что здесь выполнены первые два условия непрерывности:
1) – функция определена в данной точке;
2) 
– общий предел существует.
Но третий рубеж не пройден: , то есть предел функции в точке не равен значению данной функции в данной точке.
Таким образом, в точке функция терпит разрыв.
Второй, более грустный случай носит название разрыва первого рода со скачком . А грусть навевают односторонние пределы, которые конечны и различны . Пример изображён на втором чертеже урока. Такой разрыв возникает, как правило, в кусочно-заданных функциях , о которых уже упоминалось в статье о преобразованиях графиков .
Рассмотрим кусочную функцию
и выполним её чертёж. Как построить график? Очень просто. На полуинтервале чертим фрагмент параболы (зеленый цвет), на интервале – отрезок прямой (красный цвет) и на полуинтервале – прямую (синий цвет).
При этом в силу неравенства значение определено для квадратичной функции (зелёная точка), и в силу неравенства , значение определено для линейной функции (синяя точка):
В самом-самом тяжёлом случае следует прибегнуть к поточечному построению каждого куска графика (см. первый урок о графиках функций
).
Сейчас нас будет интересовать только точка . Исследуем её на непрерывность:
2) Вычислим односторонние пределы.
Слева у нас красный отрезок прямой, поэтому левосторонний предел: 
Справа – синяя прямая, и правосторонний предел: 
В результате получены конечные числа
, причем они не равны
. Поскольку односторонние пределы конечны и различны
: 
, то наша функция терпит разрыв первого рода со скачком
.
Логично, что разрыв не устраним – функцию действительно не доопределить и «не склеить», как в предыдущем примере.
Точки разрыва второго рода
Обычно к данной категории хитро относят все остальные случаи разрыва. Всё перечислять не буду, поскольку на практике в 99%-ти процентах задач вам встретится бесконечный разрыв – когда левосторонний или правосторонний, а чаще, оба предела бесконечны.
И, конечно же, самая напрашивающаяся картинка – гипербола в точке ноль. Здесь оба односторонних предела бесконечны: 
, следовательно, функция терпит разрыв второго рода в точке .
Я стараюсь наполнять свои статьи максимально разнообразным содержанием, поэтому давайте посмотрим на график функции , который ещё не встречался:
по стандартной схеме:
1) Функция не определена в данной точке, поскольку знаменатель обращается в ноль.
Конечно, можно сразу сделать вывод о том, что функция терпит разрыв в точке , но хорошо бы классифицировать характер разрыва, что часто требуется по условию. Для этого:
Напоминаю, что под записью понимается бесконечно малое отрицательное число
, а под записью – бесконечно малое положительное число
.
Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке . Ось ординат является вертикальной асимптотой для графика.
Не редка ситуация, когда оба односторонних предела существуют, но бесконечен только один из них, например:
Это график функции .
Исследуем на непрерывность точку :
1) Функция не определена в данной точке.
2) Вычислим односторонние пределы: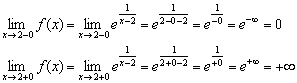
О методике вычисления таких односторонних пределов поговорим в двух последних примерах лекции, хотя многие читатели всё уже увидели и догадались.
Левосторонний предел конечен и равен нулю (в саму точку мы «не заходим»), но правосторонний предел бесконечен и оранжевая ветка графика бесконечно близко приближается к своей вертикальной асимптоте , заданной уравнением (чёрный пунктир).
Таким образом, функция терпит разрыв второго рода в точке .
Как и для разрыва 1-го рода, в самой точке разрыва функция может быть определена. Например, для кусочной функции 
смело ставим чёрную жирную точку в начале координат. Справа же – ветка гиперболы, и правосторонний предел бесконечен. Думаю, почти все представили, как выглядит этот график.
То, чего все с нетерпением ждали:
Как исследовать функцию на непрерывность?
Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:
Пример 1
Исследовать функцию 
Решение :
1) Под прицел попадает единственная точка , в которой функция не определена.
2) Вычислим односторонние пределы: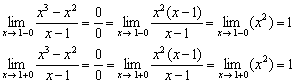
Односторонние пределы конечны и равны.
Таким образом, в точке функция терпит устранимый разрыв.
Как выглядит график данной функции?
Хочется провести упрощение 
, и вроде бы получается обычная парабола. НО
исходная функция не определена в точке , поэтому обязательна следующая оговорка:
Выполним чертёж:
Ответ : функция непрерывна на всей числовой прямой кроме точки , в которой она терпит устранимый разрыв.
Функцию можно доопределить хорошим или не очень способом, но по условию этого не требуется.
Вы скажете, пример надуманный? Ничуть. Десятки раз встречалось на практике. Почти все задачи сайта родом из реальных самостоятельных и контрольных работ.
Разделаемся с любимыми модулями:
Пример 2
Исследовать функцию 
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение
: почему-то студенты боятся и не любят функции с модулем, хотя ничего сложного в них нет. Таких вещей мы уже немного коснулись на уроке Геометрические преобразования графиков
. Поскольку модуль неотрицателен, то он раскрывается следующим образом: 
, где «альфа» – некоторое выражение. В данном случае , и наша функция должна расписаться кусочным образом:
Но дроби обоих кусков предстоит сократить на . Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке , так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие , и первое неравенство сделать строгим:
Теперь об ОЧЕНЬ ПОЛЕЗНОМ приёме решения : перед чистовым оформлением задачи на черновике выгодно сделать чертёж (независимо от того, требуется он по условию или нет). Это поможет, во-первых, сразу увидеть точки непрерывности и точки разрыва, а, во-вторых, 100%-но убережёт от ошибок при нахождении односторонних пределов.
Выполним чертёж. В соответствии с нашими выкладками, слева от точки необходимо начертить фрагмент параболы (синий цвет), а справа – кусок параболы (красный цвет), при этом функция не определена в самой точке :
Если есть сомнения, возьмите несколько значений «икс», подставьте их в функцию 
(не забывая, что модуль уничтожает возможный знак «минус») и сверьтесь с графиком.
Исследуем функцию на непрерывность аналитически:
1) Функция не определена в точке , поэтому сразу можно сказать, что не является в ней непрерывной.
2) Установим характер разрыва, для этого вычислим односторонние пределы:
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке . Ещё раз заметьте, что при нахождении пределов не имеет значения, определена функция в точке разрыва или нет.
Теперь остаётся перенести чертёж с черновика (он сделан как бы с помощью исследования;-)) и завершить задание:
Ответ : функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв первого рода со скачком.
Иногда требуют дополнительно указать скачок разрыва. Вычисляется он элементарно – из правого предела нужно вычесть левый предел: , то есть в точке разрыва наша функция прыгнула на 2 единицы вниз (о чём нам сообщает знак «минус»).
Пример 3
Исследовать функцию 
на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.
Это пример для самостоятельного решения, примерный образец решения в конце урока.
Перейдём к наиболее популярной и распространённой версии задания, когда функция состоит из трёх кусков:
Пример 4
Исследовать функцию на непрерывность и построить график функции 
.
Решение
: очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике, технику построения я достаточно подробно закомментировал в первой части статьи. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства значение принадлежит прямой (зелёная точка), и в силу неравенство значение принадлежит параболе (красная точка):
Ну вот, в принципе, всё понятно =) Осталось оформить решение. Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:
I) Исследуем на непрерывность точку
1) 
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .
Вычислим скачок разрыва как разность правого и левого пределов:
, то есть, график рванул на одну единицу вверх.
II) Исследуем на непрерывность точку
1) 
– функция определена в данной точке.
2) Найдём односторонние пределы:
– односторонние пределы конечны и равны, значит, существует общий предел.
3) 
– предел функции в точке равен значению данной функции в данной точке.
На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:
Ответ : функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.
Пример 5
Исследовать функцию на непрерывность и построить её график 
.
Это пример для самостоятельного решения, краткое решение и примерный образец оформления задачи в конце урока.
Может сложиться впечатление, что в одной точке функция обязательно должна быть непрерывной, а в другой – обязательно должен быть разрыв. На практике это далеко не всегда так. Постарайтесь не пренебрегать оставшимися примерами – будет несколько интересных и важных фишек:
Пример 6
Дана функция 
. Исследовать функцию на непрерывность в точках . Построить график.
Решение
: и снова сразу выполним чертёж на черновике:
Особенность данного графика состоит в том, что при кусочная функция задаётся уравнением оси абсцисс . Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение относится к ветке тангенса (красная точка), а значение принадлежит прямой .
Из чертежа всё понятно – функция непрерывна на всей числовой прямой, осталось оформить решение, которое доводится до полного автоматизма буквально после 3-4 подобных примеров:
I) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Вычислим односторонние пределы:
, значит, общий предел существует.
На всякий пожарный напомню тривиальный факт: предел константы равен самой константе. В данном случае предел нуля равен самому нулю (левосторонний предел).
3) 
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
II) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
И здесь – предел единицы равен самой единице.
– общий предел существует.
3) 
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
Как обычно, после исследования переносим наш чертёж на чистовик.
Ответ : функция непрерывна в точках .
Обратите внимание, что в условии нас ничего не спрашивали про исследование всей функции на непрерывность, и хорошим математическим тоном считается формулировать точный и чёткий ответ на поставленный вопрос. Кстати, если по условию не требуется строить график, то вы имеете полное право его и не строить (правда, потом преподаватель может заставить это сделать).
Небольшая математическая «скороговорка» для самостоятельного решения:
Пример 7
Дана функция 
. Исследовать функцию на непрерывность в точках . Классифицировать точки разрыва, если они есть. Выполнить чертёж.
Постарайтесь правильно «выговорить» все «слова» =) И график нарисовать поточнее, точность, она везде лишней не будет;-)
Как вы помните, я рекомендовал незамедлительно выполнять чертёж на черновике, но время от времени попадаются такие примеры, где не сразу сообразишь, как выглядит график. Поэтому в ряде случаев выгодно сначала найти односторонние пределы и только потом на основе исследования изобразить ветви. В двух заключительных примерах мы, кроме того, освоим технику вычисления некоторых односторонних пределов:
Пример 8
Исследовать на непрерывность функцию и построить её схематический график.
Решение : нехорошие точки очевидны: (обращает в ноль знаменатель показателя) и (обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование.
Похожие статьи
