Преобразование двойного интеграла от прямоугольных координат ,к полярным координатам
, связанных с прямоугольными координатами соотношениями
,
, осуществляется по формуле

Если область интегрирования
ограничена двумя лучами
,
(
), выходящими из полюса, и двумя кривыми
и
, то двойной интеграл вычисляют по формуле

Пример 1.3. Вычислить площадь фигуры, ограниченной данными линиями:
,
,
,
.

Решение. Для вычисления площади области
воспользуемся формулой:
.

Изобразим область
(рис. 1.5). Для этого преобразуем кривые:

,
,

,
.

Перейдем к полярным координатам:

,
.

В полярной системе координат область
описывается уравнениями:

1.2. Тройные интегралы

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

В декартовых координатах тройной интеграл обычно записывают так:

Если
, то тройной интеграл по областичисленно равен объему тела:

Вычисление тройного интеграла

Пусть область интегрирования ограничена снизу и сверху соответственно однозначными непрерывными поверхностями
,
, причем проекция областина координатную плоскость
есть плоская область
(рис. 1.6).

Тогда при фиксированных значениях
соответствующие аппликатыточек областиизменяются в пределах.

Тогда получаем:

Если, кроме того, проекция
определяется неравенствами

,
,

где
- однозначные непрерывные функции на
, то

Пример 1.4. Вычислить
, где- тело, ограниченное плоскостями:

,
,
,
(
,
,
).

Решение. Областью интегрирования является пирамида (рис. 1.7). Проекция области есть треугольник
, ограниченный прямыми
,
,
(рис. 1.8). При
аппликаты точек
удовлетворяют неравенству
, поэтому

Расставляя пределы интегрирования для треугольника
, получим

Тройной интеграл в цилиндрических координатах

При переходе от декартовых координат
к цилиндрическим координатам
(рис. 1.9), связанных с
соотношениями
,
,
, причем

,
,,

тройной интеграл преобразуется:

Пример 1.5. Вычислить объем тела, ограниченного поверхностями:
,
,
.

Решение. Искомый объем тела равен
.

Областью интегрирования является часть цилиндра, ограниченного снизу плоскостью
, а сверху плоскостью
(рис. 1.10). Проекция областиесть круг
с центром в начале координат и единичном радиусом.

Перейдем к цилиндрическим координатам.
,
,
. При
аппликаты точек
, удовлетворяют неравенству

или в цилиндрических координатах:

Область
, ограниченная кривой
, примет вид, или
, при этом полярный угол
. В итоге имеем

2. Элементы теории поля

Напомним предварительно способы вычисления криволинейных и поверхностных интегралов.

Вычисление криволинейного интеграла по координатам от функций, определенных на кривой , сводится к вычислению определенного интеграла вида

если кривая задана параметрическии
соответствует начальной точке кривой, а
- ее конечной точке.

Вычисление поверхностного интеграла от функции
, определенной на двусторонней поверхности, сводится к вычислению двойного интеграла, например, вида

если поверхность , заданная уравнением
, однозначно проецируется на плоскость
в область
. Здесь- угол между единичным вектором нормалик поверхностии осью
:

Требуемая условиями задачи сторона поверхности определяется выбором соответствующего знака в формуле (2.3).

Определение 2.1. Векторным полем
называется векторная функция точки
вместе с областью ее определения:

Векторное поле
характеризуется скалярной величиной –дивергенцией:

Определение 2.2. Потоком векторного поля
через поверхность называется поверхностный интеграл:

где - единичный вектор нормали к выбранной стороне поверхности, а
- скалярное произведение векторови.

Определение 2.3. Циркуляцией векторного поля

по замкнутой кривой называется криволинейный интеграл

где
.

Формула Остроградского-Гаусса устанавливает связь между потоком векторного поля через замкнутую поверхность и дивергенцией поля:

где - поверхность, ограниченная замкнутым контуром , а - единичный вектор нормали к этой поверхности. Направление нормали должно быть согласовано с направлением обхода контура .

Пример 2.1. Вычислить поверхностный интеграл

где - внешняя часть конуса
(
), отсекаемая плоскостью
(рис 2.1).

Решение. Поверхность однозначно проецируется в область
плоскости
, и интеграл вычисляется по формуле (2.2).

Единичный вектор нормали к поверхности найдем по формуле (2.3):

Здесь в выражении для нормали выбран знак плюс, так как угол между осью
и нормалью- тупой и, следовательно,
должен быть отрицательным. Учитывая, что
, на поверхностиполучаем

Область
есть круг
. Поэтому в последнем интеграле переходим к полярным координатам, при этом
,
:

Пример 2.2. Найти дивергенцию и ротор векторного поля
.

Решение. По формуле (2.4) получаем

Ротор данного векторного поля находим по формуле (2.5)

Пример 2.3. Найти поток векторного поля
через часть плоскости:
, расположенную в первом октанте (нормаль образует острый угол с осью
).

Решение. В силу формулы (2.6)

Изобразим часть плоскости :
, расположенную в первом октанте. Уравнение данной плоскости в отрезках имеет вид

(рис. 2.3). Вектор нормали к плоскости имеет координаты:
, единичный вектор нормали

,
, откуда
, следовательно,

где
- проекция плоскостина
(рис. 2.4).

Пример 2.4. Вычислить поток векторного поля через замкнутую поверхность, образованную плоскостью
и частью конуса
(
) (рис. 2.2).

Решение. Воспользуемся формулой Остроградского-Гаусса (2.8)

Найдем дивергенцию векторного поля по формуле (2.4):

где
- объем конуса, по которому ведется интегрирование. Воспользуемся известной формулой для вычисления объема конуса
(- радиус основания конуса,- его высота). В нашем случае получаем
. Окончательно получаем

Пример 2.5. Вычислить циркуляцию векторного поля
по контуру , образованному пересечением поверхностей
и
(
). Проверить результат по формуле Стокса.

Решение. Пересечением указанных поверхностей является окружность
,
(рис. 2.1). Направление обхода выбирается обычно так, чтобы ограниченная им область оставалась слева. Запишем параметрические уравнения контура :

откуда

причем параметр изменяется отдо
. По формуле (2.7) с учетом (2.1) и (2.10) получаем

Применим теперь формулу Стокса (2.9). В качестве поверхности , натянутой на контур , можно взять часть плоскости
. Направление нормали
к этой поверхности согласуется с направлением обхода контура . Ротор данного векторного поля вычислен в примере 2.2:
. Поэтому искомая циркуляция

где
- площадь области
.
- круг радиуса
, откуда

Пусть имеем две прямоугольные системы координат в пространстве и
, и систему функций

(1)

которые устанавливают взаимно-однозначное соответствие между точками некоторых областей
и
в этих системах координат. Предположим, что функции системы (1) имеют в
непрерывные частные производные. Определитель, составленный из этих частных производных

называют якобианом (или определителем Якоби) системы функций (1). Мы будем предполагать, что
в
.

В сделанных выше предположениях имеет место следующая общая формула замены переменных в тройном интеграле:

Как и в случае двойного интеграла, взаимная однозначность системы (1) и условие
могут нарушаться в отдельных точках, на отдельных линиях и на отдельных поверхностях.

Система функций (1) каждой точке
ставит в соответствие единственную точку
. Эти три числа
называют криволинейными координатами точки. Точки пространства
, для которых одна из этих координат сохраняет постоянное значение, образуют т.н. координатную поверхность.

II Тройной интеграл в цилиндрических координатах

Цилиндрическая система координат (ЦСК) определяется плоскостью
, в которой задана полярная система координат и осью
, перпендикулярной этой плоскости. Цилиндрическими координатами точки
, где
– полярные координаты точки– проекции точкина плоскость
, а– это координаты проекции точкина ось
или
.

В плоскости
введем обычным образом декартовы координаты, ось аппликат направим по оси
ЦСК. Теперь нетрудно получить формулы, связывающие цилиндрические координаты с декартовыми:

(3)

Эти формулы отображают областьна все пространство
.

Координатными поверхностями в рассматриваемом случае будут:

1)
– цилиндрические поверхности с образующими, парал-лельными оси
, направляющими которых служат окружности в плоскости
, с центром в точке;

2)

;

3)
– плоскости, параллельные плоскости
.

Якобиан системы (3):

Общая формула в случае ЦСК принимает вид:

Замечание 1 . Переход к цилиндрическим координатам рекомендуется в случае, когда область интегрирования – это круговые цилиндр или конус, или параболоид вращения (или их части), причем ось этого тела совпадает с осью аппликат
.

Замечание 2. Цилиндрические координаты можно обобщить так же, как и полярные координаты на плоскости.

Пример 1. Вычислить тройной интеграл от функции

по области
, представляющей собой внутреннюю часть цилиндра
, ограниченную конусом
и параболоидом
.

Решение. Эту область мы уже рассматривали в §2, пример 6, и получили стандартную запись в ДПСК. Однако, вычисление интеграла в этой области затруднительно. Перейдем в ЦСК:

Проекция
тела
на плоскость
– это круг
. Следовательно, координатаизменяется от 0 до
, а– от0 до R . Через произвольную точку
проведем прямую, параллельную оси
. Прямая войдет в
на конусе, а выйдет на параболоиде. Но конус
имеет в ЦСК уравнение
, а параболоид
– уравнение
. Итак, имеем

III Тройной интеграл в сферических координатах

Сферическая система координат (ССК) определяется плоскостью
, в которой задана ПСК, и осью
, перпендикулярной плоскости
.

Сферическими координатами точки пространства называют тройку чисел
, где– полярный угол проекции точки на плоскость
,– угол между осью
и вектором
и
.

В плоскости
введем декартовы координатные оси
и
обычным образом, а ось аппликат совместим с осью
. Формулы, связывающие сферические координаты с декартовыми таковы:

(4)

Эти формулы отображают область на всё пространство
.

Якобиан системы функций (4):

Координатные поверхности составляют три семейства:

1)
– концентрические сферы с центром в начале координат;

2)
– полуплоскости, проходящие через ось
;

3)
– круговые конусы с вершиной в начале координат, осью которых служит ось
.

Формула перехода в ССК в тройном интеграле:

Замечание 3. Переход в ССК рекомендуется, когда область интегрирования – это шар или его часть. При этом уравнение сферы
переходит в. Как и ЦСК, рассмотренная ранее, ССК «привязана» к оси
. Если центр сферы смещён на радиус вдоль координатной оси, то наиболее простое сферическое уравнение получим при смещении вдоль оси
:

Замечание 4. Возможно обобщение ССК:

с якобианом
. Эта система функций переведет эллипсоид

в «параллелепипед»

Пример 2. Найти среднее расстояние точек шара радиуса от его центра.

Решение. Напомним, что среднее значение функции
в области
– это тройной интеграл от функции по области деленный на объём области. В нашем случае

Итак, имеем

Тройные интегралы. Вычисление объема тела.
Тройной интеграл в цилиндрических координатах

Три дня в деканате покойник лежал, в штаны Пифагора одетый,
В руках Фихтенгольца он томик держал, что сжил его с белого света,
К ногам привязали тройной интеграл, и в матрицу труп обернули,
А вместо молитвы какой-то нахал прочёл теорему Бернулли.

Тройные интегралы – это то, чего уже можно не бояться =) Ибо если Вы читаете сей текст, то, скорее всего, неплохо разобрались с теорией и практикой «обычных» интегралов , а также двойными интегралами . А там, где двойной, неподалёку и тройной:

И в самом деле, чего тут опасаться? Интегралом меньше, интегралом больше….

Разбираемся в записи:

– значок тройного интеграла;
– подынтегральная функция трёх переменных ;
– произведение дифференциалов.
– область интегрирования.

Особо остановимся на области интегрирования . Если в двойном интеграле она представляет собой плоскую фигуру , то здесь – пространственное тело , которое, как известно, ограничено множеством поверхностей . Таким образом, помимо вышеуказанного вы должны ориентироваться в основных поверхностях пространства и уметь выполнять простейшие трёхмерные чертежи.

Некоторые приуныли, понимаю…. Увы, статью нельзя озаглавить «тройные интегралы для чайников», и кое-что знать/уметь нужно. Но ничего страшного – весь материал изложен в предельно доступной форме и осваивается в кратчайшие сроки!

Что значит вычислить тройной интеграл и что это вообще такое?

Вычислить тройной интеграл – это значит найти ЧИСЛО :

В простейшем случае, когда , тройной интеграл численно равен объёму тела . И действительно, в соответствии с общим смыслом интегрирования , произведение равно бесконечно малому объёму элементарного «кирпичика» тела. А тройной интеграл как раз и объединяет все эти бесконечно малые частички по области , в результате чего получается интегральное (суммарное) значение объёма тела: .

Кроме того, у тройного интеграла есть важные физические приложения . Но об этом позже – во 2-й части урока, посвящённой вычислениям произвольных тройных интегралов , у которых функция в общем случае отлична от константы и непрерывна в области . В данной же статье детально рассмотрим задачу нахождения объёма, которая по моей субъективной оценке встречается в 6-7 раз чаще.

Как решить тройной интеграл?

Ответ логично вытекает из предыдущего пункта. Необходимо определить порядок обхода тела и перейти к повторным интегралам . После чего последовательно расправиться с тремя одиночными интегралами.

Как видите, вся кухня очень и очень напоминает двойные интегралы , с тем отличием, что сейчас у нас добавилась дополнительная размерность (грубо говоря, высота). И, наверное, многие из вас уже догадались, как решаются тройные интегралы.

Развеем оставшиеся сомнения:

Пример 1

Пожалуйста, перепишите столбиком на бумагу:

И ответьте на следующие вопросы. Знаете ли Вы, какие поверхности задают эти уравнения? Понятен ли Вам неформальный смысл этих уравнений? Представляете ли Вы, как данные поверхности расположены в пространстве?

Если Вы склоняетесь к общему ответу «скорее нет, чем да», то обязательно проработайте урок , иначе дальше будет не продвинуться!

Решение : используем формулу .

Для того чтобы выяснить порядок обхода тела и перейти к повторным интегралам нужно (всё гениальное просто) понять, что это за тело. И такому пониманию во многих случаях здОрово способствуют чертёжи.

По условию тело ограничено несколькими поверхностями. С чего начать построение? Предлагаю следующий порядок действий:

Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость . Первый раз сказал, как эта проекция называется, lol =)

Коль скоро проецирование проводится вдоль оси , то в первую очередь целесообразно разобраться с поверхностями , которые параллельны данной оси. Напоминаю, что уравнения таких поверхностей не содержат буквы «зет» . В рассматриваемой задаче их три:

– уравнение задаёт координатную плоскость , которая проходит через ось ;
– уравнение задаёт координатную плоскость , которая проходит через ось ;
– уравнение задаёт плоскость «плоскую» прямую параллельно оси .

Скорее всего, искомая проекция представляет собой следующий треугольник:

Возможно, не все до конца поняли, о чём речь. Представьте, что из экрана монитора выходит ось и утыкается прямо в вашу переносицу (т.е. получается, что вы смотрите на 3-мерный чертёж сверху) . Исследуемое пространственное тело находится в бесконечном трёхгранном «коридоре» и его проекция на плоскость вероятнее всего представляет собой заштрихованный треугольник.

Обращаю особое внимание, что пока мы высказали лишь предположение о проекции и оговорки «скорее всего», «вероятнее всего» были не случайны. Дело в том, что проанализированы ещё не все поверхности и может статься так, что какая-нибудь из них «оттяпает» часть треугольника. В качестве наглядного примера напрашивается сфера с центром в начале координат радиусом мЕньшим единицы, например, сфера – её проекция на плоскость (круг ) не полностью «накроет» заштрихованную область, и итоговая проекция тела будет вовсе не треугольником (круг «срежет» ему острые углы) .

На втором этапе выясняем, чем тело ограничено сверху, чем снизу и выполняем пространственный чертёж. Возвращаемся к условию задачи и смотрим, какие поверхности остались. Уравнение задаёт саму координатную плоскость , а уравнение – параболический цилиндр , расположенный над плоскостью и проходящий через ось . Таким образом, проекция тела действительно представляет собой треугольник.

Кстати, здесь обнаружилась избыточность условия – в него было не обязательно включать уравнение плоскости , поскольку поверхность , касаясь оси абсцисс, и так замыкает тело. Интересно отметить, что в этом случае мы бы не сразу смогли начертить проекцию – треугольник «прорисовался» бы только после анализа уравнения .

Аккуратно изобразим фрагмент параболического цилиндра:

После выполнения чертежей с порядком обхода тела никаких проблем!

Сначала определим порядок обхода проекции (при этом ГОРАЗДО УДОБНЕЕ ориентироваться по двумерному чертежу). Это делается АБСОЛЮТНО ТАК ЖЕ , как и в двойных интегралах ! Вспоминаем лазерную указку и сканирование плоской области. Выберем «традиционный» 1-й способ обхода:

Далее берём в руки волшебный фонарик, смотрим на трёхмерный чертёж и строго снизу вверх просвечиваем пациента. Лучи входят в тело через плоскость и выходят из него через поверхность . Таким образом, порядок обхода тела:

Перейдём к повторным интегралам:

1) Начать следует с «зетового» интеграла. Используем формулу Ньютона-Лейбница :

Подставим результат в «игрековый» интеграл:

Что получилось? По существу решение свелось к двойному интегралу, и именно – к формуле объёма цилиндрического бруса ! Дальнейшее хорошо знакомо:

Обратите внимание на рациональную технику решения 3-го интеграла.

Ответ :

Вычисления всегда можно записать и «одной строкой»:

Но с этим способом будьте осторожнее – выигрыш в скорости чреват потерей качества, и чем труднее пример, тем больше шансов допустить ошибку.

Ответим на важный вопрос:

Нужно ли делать чертёжи, если условие задачи не требует их выполнения?

Можно пойти четырьмя путями:

1) Изобразить проекцию и само тело. Это самый выигрышный вариант – если есть возможность выполнить два приличных чертежа, не ленитесь, делайте оба чертежа. Рекомендую в первую очередь.

2) Изобразить только тело. Годится, когда у тела несложная и очевидная проекция. Так, например, в разобранном примере хватило бы и трёхмерного чертежа. Однако тут есть и минус – по 3D-картинке неудобно определять порядок обхода проекции, и этот способ я бы советовал только людям с хорошим уровнем подготовки.

3) Изобразить только проекцию. Тоже неплохо, но тогда обязательны дополнительные письменные комментарии, чем ограничена область с различных сторон. К сожалению, третий вариант зачастую бывает вынужденным – когда тело слишком велико либо его построение сопряжено с иными трудностями. И такие примеры мы тоже рассмотрим.

4) Обойтись вообще без чертежей. В этом случае нужно представлять тело мысленно и закомментировать его форму/расположение письменно. Подходит для совсем простых тел либо задач, где выполнение обоих чертежей затруднительно. Но всё же лучше сделать хотя бы схематический рисунок, поскольку «голое» решение могут и забраковать.

Следующее тело для самостоятельного дела:

Пример 2

С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями

В данном случае область интегрирования задана преимущественно неравенствами, и это даже лучше – множество неравенств задаёт 1-й октант, включая координатные плоскости, а неравенство – полупространство , содержащее начало координат (проверьте) + саму плоскость. «Вертикальная» плоскость рассекает параболоид по параболе и на чертеже желательно построить данное сечение. Для этого нужно найти дополнительную опорную точку, проще всего – вершину параболы (рассматриваем значения и рассчитываем соответствующее «зет») .

Продолжаем разминаться:

Пример 3

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Выполнить чертёж.

Решение : формулировка «выполнить чертёж» даёт нам некоторую свободу, но, скорее всего, подразумевает выполнение пространственного чертежа. Однако и проекция тоже не помешает, тем более, она здесь не самая простая.

Придерживаемся отработанной ранее тактики – сначала разберёмся с поверхностями , которые параллельны оси аппликат. Уравнения таких поверхностей не содержат в явном виде переменную «зет»:

– уравнение задаёт координатную плоскость , проходящую через ось (которая на плоскости определяется «одноимённым» уравнением ) ;
– уравнение задаёт плоскость , проходящую через «одноимённую» «плоскую» прямую параллельно оси .

Искомое тело ограниченно плоскостью снизу и параболическим цилиндром сверху:

Составим порядок обхода тела, при этом «иксовые» и «игрековые» пределы интегрирования, напоминаю, удобнее выяснять по двумерному чертежу:

Таким образом:

При интегрировании по «игрек» – «икс» считается константой, поэтому константу целесообразно сразу вынести за знак интеграла.

Ответ :

Да, чуть не забыл, в большинстве случаев полученный результат малополезно (и даже вредно) сверять с трёхмерным чертежом, поскольку с большой вероятностью возникнет иллюзия объёма , о которой я рассказал ещё на уроке Объем тела вращения . Так, оценивая тело рассмотренной задачи, лично мне показалось, что в нём гораздо больше 4 «кубиков».

Следующий пример для самостоятельного решения:

Пример 4

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость .

Примерный образец оформления задачи в конце урока.

Не редкость, когда выполнение трёхмерного чертежа затруднено:

Пример 5

С помощью тройного интеграла найти объём тела, заданного ограничивающими его поверхностями

Решение : проекция здесь несложная, но вот над порядком её обхода нужно подумать. Если выбрать 1-й способ, то фигуру придётся разделить на 2 части, что неиллюзорно грозит вычислением суммы двух тройных интегралов. В этой связи гораздо перспективнее выглядит 2-й путь. Выразим и изобразим проекцию данного тела на чертеже:

Прошу прощения за качество некоторых картинок, я их вырезаю прямо из собственных рукописей.

Выбираем более выгодный порядок обхода фигуры:

Теперь дело за телом. Снизу оно ограничено плоскостью , сверху – плоскостью , которая проходит через ось ординат. И всё бы было ничего, но последняя плоскость слишком крутА и построить область не так-то просто. Выбор тут незавиден: либо ювелирная работа в мелком масштабе (т.к. тело достаточно тонкое), либо чертёж высотой порядка 20 сантиметров (да и то, если вместится).

Но есть и третий, исконно русский метод решения проблемы – забить =) А вместо трёхмерного чертежа обойтись словесным описанием: «Данное тело ограничено цилиндрами и плоскостью сбоку, плоскостью – снизу и плоскостью – сверху».

«Вертикальные» пределы интегрирования, очевидно, таковы:

Вычислим объём тела, не забывая, что проекцию мы обошли менее распространённым способом:

Ответ :

Как вы заметили, предлагаемые в задачах тела не дороже сотни баксов часто ограничены плоскостью снизу. Но это не есть какое-то правило, поэтому всегда нужно быть начеку – может попасться задание, где тело расположено и под плоскостью . Так, например, если в разобранной задаче вместо рассмотреть плоскость , то исследованное тело симметрично отобразится в нижнее полупространство и будет ограничено плоскостью снизу, а плоскостью – уже сверху!

Легко убедиться, что получится тот же самый результат:

(помним, что тело нужно обходить строго снизу вверх! )

Кроме того, «любимая» плоскость может оказаться вообще не при делах, простейший пример: шар, расположенный выше плоскости – при вычислении его объёма уравнение не понадобится вообще.

Все эти случаи мы рассмотрим, а пока аналогичное задание для самостоятельного решения:

Пример 6

С помощью тройного интеграла найти объём тела, ограниченного поверхностями

Краткое решение и ответ в конце урока.

Переходим ко второму параграфу с не менее популярными материалами:

Тройной интеграл в цилиндрических координатах

Цилиндрические координаты – это, по сути, полярные координаты в пространстве.
В цилиндрической системе координат положение точки пространства определяется полярными координатами и точки – проекции точки на плоскость и аппликатой самой точки .

Переход от трёхмерной декартовой системы к цилиндрической системе координат осуществляется по следующим формулам:

Применительно к нашей теме преобразование выглядит следующим образом:

И, соответственно, в упрощённом случае, который мы рассматриваем в этой статье:

Главное, не забывать про дополнительный множитель «эр» и правильно расставлять полярные пределы интегрирования при обходе проекции:

Пример 7

Решение : придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых отсутствует переменная «зет». Оно здесь одно. Проекция цилиндрической поверхности на плоскость представляет собой «одноимённую» окружность .

Плоскости ограничивают искомое тело снизу и сверху («высекают» его из цилиндра) и проецируются в круг :

На очереди трёхмерный чертёж. Основная трудность состоит в построении плоскости , которая пересекает цилиндр под «косым» углом, в результате чего получается эллипс . Уточним данное сечение аналитически: для этого перепишем уравнение плоскости в функциональном виде и вычислим значения функции («высоту») в напрашивающихся точках , которые лежат на границе проекции:

Отмечаем найдённые точки на чертеже и аккуратно (а не так, как я =)) соединяем их линией:

Проекция тела на плоскость представляет собой круг, и это весомый аргумент в пользу перехода к цилиндрической системе координат:

Найдём уравнения поверхностей в цилиндрических координатах:

Теперь следует выяснить порядок обхода тела.

Сначала разберёмся с проекцией. Как определить её порядок обхода? ТОЧНО ТАК ЖЕ, как и при вычислении двойных интегралов в полярных координатах . Здесь он элементарен:

«Вертикальные» пределы интегрирования тоже очевидны – входим в тело через плоскость и выходим из него через плоскость :

Перейдём к повторным интегралам:

При этом множитель «эр» сразу ставим в «свой» интеграл.

Веник как обычно легче сломать по прутикам:

Сносим результат в следующий интеграл:

А тут не забываем, что «фи» считается константой. Но это до поры до времени:

Ответ :

Похожее задание для самостоятельного решения:

Пример 8

Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями . Выполнить чертёжи данного тела и его проекции на плоскость .

Примерный образец чистового оформления в конце урока.

Обратите внимание, что в условиях задач ни слова не сказано о переходе к цилиндрической системе координат, и несведущий человек будет бодаться с трудными интегралами в декартовых координатах. …А может и не будет – ведь есть третий, исконно русский способ решения проблем =)

Всё только начинается! …в хорошем смысле: =)

Пример 9

С помощью тройного интеграла найти объем тела, ограниченного поверхностями

Скромно и со вкусом.

Решение : данное тело ограничено конической поверхностью и эллиптическим параболоидом . Читатели, которые внимательно ознакомились с материалами статьи Основные поверхности пространства , уже представили, как выглядит тело, но на практике часто встречаются более сложные случаи, поэтому я проведу подробное аналитическое рассуждение.

Сначала найдём линии, по которым пересекаются поверхности. Составим и решим следующую систему:

Из 1-го уравнения почленно вычтем второе:

В результате получено два корня:

Подставим найденное значение в любое уравнение системы:
, откуда следует, что
Таким образом, корню соответствует единственная точка – начало координат. Естественно – ведь вершины рассматриваемых поверхностей совпадают.

Теперь подставим второй корень – тоже в любое уравнение системы:

Каков геометрический смысл полученного результата? «На высоте» (в плоскости ) параболоид и конус пересекаются по окружности – единичного радиуса с центром в точке .

При этом «чаша» параболоида вмещает в себя «воронку» конуса, поэтому образующие конической поверхности следует прочертить пунктиром (за исключением отрезка дальней от нас образующей, который виден с данного ракурса):

Проекцией тела на плоскость является круг с центром в начале координат радиуса 1, который я даже не удосужился изобразить ввиду очевидности данного факта (однако письменный комментарий делаем!) . Кстати, в двух предыдущих задачах на чертёж проекции тоже можно было бы забить, если бы не условие.

При переходе к цилиндрическим координатам по стандартным формулам неравенство запишется в простейшем виде и с порядком обхода проекции никаких проблем:

Найдём уравнения поверхностей в цилиндрической системе координат:

Так как в задаче рассматривается верхняя часть конуса, то из уравнения выражаем:

«Сканируем тело» снизу вверх. Лучи света входят в него через эллиптический параболоид и выходят через коническую поверхность . Таким образом, «вертикальный» порядок обхода тела:

Остальное дело техники:

Ответ :

Не редкость, когда тело задаётся не ограничивающими его поверхностями, а множеством неравенств:

Пример 10

Геометрический смысл пространственных неравенств я достаточно подробно разъяснил в той же справочной статье – Основные поверхности пространства и их построение .

Данная задача хоть и содержит параметр, но допускает выполнение точного чертежа, отражающего принципиальный вид тела. Подумайте, как выполнить построение. Краткое решение и ответ – в конце урока.

…ну что, ещё парочку заданий? Думал закончить урок, но прямо так и чувствую, что вы хотите ещё =)

Пример 11

С помощью тройного интеграла вычислить объём заданного тела:
, где – произвольное положительное число.

Решение : неравенство задаёт шар с центром в начале координат радиуса , а неравенство – «внутренность» кругового цилиндра с осью симметрии радиуса . Таким образом, искомое тело ограничено круговым цилиндром сбоку и симметричными относительно плоскости сферическими сегментами сверху и снизу.

Принимая за базовую единицу измерения, выполним чертёж:

Точнее, его следует назвать рисунком, поскольку пропорции по оси я выдержал не очень-то хорошо. Однако, справедливости ради, по условию вообще не требовалось ничего чертить и такой иллюстрации оказалось вполне достаточно.

Обратите внимание, что здесь не обязательно выяснять высоту, на которой цилиндр высекает из шара «шапки» – если взять в руки циркуль и наметить им окружность с центром в начале координат радиуса 2 см, то точки пересечения с цилиндром получатся сами собой.

Записывается тройной интеграл так:

Вычислить тройной интеграл - значит найти число, равное объёму тела V или, что то же самое - области V .

Практически каждый может понять смысл вычисления тройного интеграла "на своей шкуре". Точнее - "под шкурой", а ещё точнее - по своим органам дыхания - лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол - пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое "огромное количество малостей" математически как раз и формулируется понятие тройного интеграла.

Почему именно тройной интеграл служит для нахождения объёма тела V ? Пусть область V разбита на n произвольных областей Δv i , причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём. В каждой такой маленькой области выбрана произвольная точка M i , а f (M i ) - значение функции f (M ) в этой точке. Теперь будем максимально увеличивать число таких маленьких областей, а наибольший диаметр Δv i - наоборот, уменьшать. Можем составить интегральную сумму вида

Если функция f (M ) = f (x , y , z ) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом .

В этом случае функция f (M ) = f (x , y , z ) называется интегрируемой в области V ; V - областью интегрирования; x , y , z - переменными интегрирования, dv (или dx dy dz ) - элементом объёма.

Вычисление тройного интеграла путём уменьшения кратности

Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.

Рассмотрим трёхмерную область V . Снизу и сверху (то есть по высоте) эта область ограничена поверхностями z = z 1 (x , y ) и z = z 2 (x , y ) . С боковых сторон (то есть по ширине) область ограничена поверхностями y = y 1 (x ) и y = y 2 (x ) . И, наконец, по глубине (если Вы смотрите на область в направлении оси Ox ) - поверхностями x = a и x = b

Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной. Она правильна тогда, когда прямая, параллельная оси Oz , пересекает границу области V не более чем в двух точках. Правильными трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже - прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.

Чтобы наглядно представить отличие правильности от неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На рисунке ниже - пример неправильной области V - однополостный гиперболоид, поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.

Мы будем рассматривать только правильные области.

Итак, область V - правильная. Тогда для любой функции f (x , y , z ) , непрерывной в области V , справедлива формула

Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению внутреннего определённого интеграла по переменной z (при постоянных x и y ) и внешнего двойного интеграла по двумерной области D .

Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:

Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.

Вычисляются эти интегралы от самого внутреннего (по переменной z ) к самому внешнему (по переменной x ). Для удобства восприятия последовательности вычислений три "вложенных" интеграла можно записать так:

Из этой записи уже однозначно видно, что:

сначала нужно интегрировать функцию f (x , y , z ) по переменной z , а в качестве пределов интегрирования взять уравнения z = z 1 (x , y ) и z = z 2 (x , y ) поверхностей ограничивающих область V снизу и сверху;
y y = y 1 (x ) и y = y 2 (x ) поверхностей, ограничивающих область V с боковых сторон;
получившийся на предыдущем шаге результат интегрировать по переменной x , а в качестве пределов интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.

Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:

Вычислим второй интеграл - по переменной y :

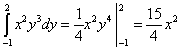x :

Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.

Пример 2. Вычислить тройной интеграл

где V - параллелепипед, ограниченный плоскостями x = − 1 , x = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:

Вычисляем интеграл "в серединке" - по переменной y . Получаем;

Теперь вычисляем самый внешний интеграл - по переменной x :

Ответ: данный тройной интеграл равен -2.

Пример 3. Вычислить тройной интеграл

где V x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 . Область V проецируется на плоскость xOy в треугольник D , как показано на рисунке ниже.

Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0 . Чтобы получить верхний предел, выразим z из x + y + z = 1 . Получаем 1 − x − y . Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0 . Для получения верхнего предела выразим y из x + y + z = 1 , считая при этом, что z = 0 (так как линия расположена в плоскости xOy ). Получаем: 1 − x .

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

y . Получаем:

x :

Ответ: данный тройной интеграл равен 1/8.

Вычислить тройной интеграл самостоятельно, а затем посмотреть решение

Пример 4. Вычислить тройной интеграл

где V - пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 .

Расстановка пределов интегрирования при переходе к последовательности трёх интегралов

Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность. В первом примере область интегрирования V представляла собой параллелепипед, с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно заданы уравнениями плоскостей. Во втором примере - пирамида: здесь уже требовалось чуть больше подумать и выразить один из пределов из уравнения. А если область V ограничивают не плоские поверхности? Нужно, конечно, определённым образом осмотреть область V .

Начнём с примера "пострашнее", чтобы почувствовать "обстановку, приближенную к боевой".

Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V - эллипсоид

Решение. Пусть центр эллипсоида - начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z :

Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy . Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z :

Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:

Чтобы получить нижний предел интегрирования по переменной y , нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:

Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:

Что касается интегрирования по переменной x , то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a : x 1 = − a и x 2 = a .

Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:

где "игрек первое", "игрек второе", "зет первое" и "зет второе" - полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc /3 .

Следующие примеры - не такие страшные, как только что рассмотренный. При этом они предполагают не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте, чему вы научились, следя за решением "страшного" примера. Думать при расстановке пределов всё равно придётся.

Пример 6. Вычислить тройной интеграл

если область интегрирования ограничена плоскостями x + y = 1 , x + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .

Решение. "Курортный" пример по сравнению с примером 5, так как пределы интегрирования по "игрек" и "зет" определены однозначно. Но придётся разобраться с пределами интегрирования по "иксу". Проекцией области интегрирования на плоскость xOy является трапеция ABCD .

В этом примере выгоднее проецировать трапецию на ось Oy , иначе, чтобы вычислить тройной интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по "иксу" чисто алгебраически. Для этого выразим "икс" из первого и второго уравнений, данных в условии примера. Из первого уравения получаем нижний предел 1 − y , из второго - верхний 4 − 2y . Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

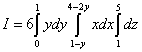Внимание! В этом примере самый внешний интеграл - не по переменной "икс", а по переменной "игрек", а "средний" - по переменной "икс"! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox , на на ось Oy .

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

Вычисляем средний интеграл - по переменной x . Получаем:

Наконец, вычисляем самый внешний интеграл - по переменной y :

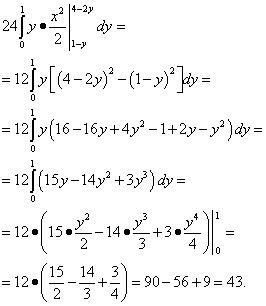
Ответ: данный тройной интеграл равен 43.

Пример 7. Вычислить тройной интеграл

если область интегрирования ограничена поверхностями x = 0 , y = 0 , z = 2 , x + y + z = 4 .

Решение. Область V (пирамида MNRP ) является правильной. Проекцией области V на плоскость xOy является треугольник AOB .

Нижние пределы интегрирования по всем переменным заданы в условии примера. Найдём верхний предел интегирования по "иксу". Для этого выразим "икс" из четвёртого уравнения, считая "игрек" равным нулю, а "зет" равным двум. Получаем x = 2 . Найдём верхний предел интегирования по "игреку". Для этого выразим "игрек" из того же четвёртого уравнения, считая "зет" равным двум, а "икс" - переменной величиной. Получаем y = 2 − x . И, наконец, найдём верхний предел интегрирования по переменной "зет". Для этого выразим "зет" из того же четвёртого уравнения, считая "игрек" и "зет" переменными величинами. Получаем z = 4 − x − y .

Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

Вычисляем средний интеграл - по переменной y . Получаем:

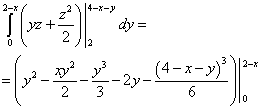Вычисляем самый внешний интеграл - по переменной x и окончательно находим данный тройной интеграл:

Ответ: данный тройной интеграл равен 2.

Замена переменных в тройном интеграле и цилиндрические координаты

Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r , φ , z ), где r - расстояние от начала координат до проекции N точки M на плоскость xOy , φ - угол между вектором ON и положительным направлением оси Ox , z - аппликата точки M (рисунок ниже).

Прямоугольные координаты x , y , z с цилиндрическими координатами r , φ , z связывают формулы

x = r cosφ ,

y = r sinφ ,

z = z .

Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r , φ , z :

То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:

Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:

Пример 8. Вычислить тройной интеграл

переходом к цилиндрическим координатам, где V - область, ограниченная поверхностями и .

Решение. Так как область V на плоскость xOy проектируется в круг , то координата φ изменяется в пределах от 0 до 2π , а координата r - от r =0 до r =1. Постоянному значению в пространстве соответствует цилиндр . Рассматривая пересечение этого цилиндра с областью V , получаем изменение ординаты z от z = r ² до z = 1 . Переходим к цилиндрическим координатам и получаем.

1. Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).

Пусть M(x, y, z) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел - полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид

Якобиан отображения (8)

Пример 2 .

Вычислить интеграл

где T - область, ограниченная поверхностями

Решение. Перейдём в интеграле к сферическим координатам по формулам (9). Тогда область интегрирования можно задать неравенствами

А, значит,

Пример 3 Найти объём тела, ограниченного:

x 2 +y 2 +z 2 =8,

Имеем: x 2 +y 2 +z 2 =8 - сфера радиуса R= v8 с центром в точке O(000),

Верхняя часть конуса z 2 =x 2 +y 2 с осью симметрии Оz и вершиной в точке O (рис. 2.20).

Найдем линию пересечения сферы и конуса:

И так как по условию z ? 0, то

Окружность R=2, лежащая в плоскости z=2.

Поэтому согласно (2.28)

где область U ограничена сверху

(часть сферы),

(часть конуса);

область U проектируется на плоскости Оху в область D - круг радиуса 2.

Следовательно, целесообразно перейти в тройном интеграле к цилиндрическим координатам, используя формулы (2.36):

Пределы изменения ц, r находим по области D v полный круг R=2 с центром в точке О, тем самым: 0?ц?2р, 0?r?2. Таким образом, область U в цилиндрических координатах задается следующими неравенствами: