Transformation av dubbelintegral av rektangulära koordinater,  till polära koordinater
till polära koordinater  , relaterade till rektangulära koordinater av relationerna
, relaterade till rektangulära koordinater av relationerna  ,
, , utförs enligt formeln
, utförs enligt formeln
Om domänen för integration  begränsad till två strålar
begränsad till två strålar  ,
, (
( ), som kommer ut ur stolpen, och två kurvor
), som kommer ut ur stolpen, och två kurvor  Och
Och  , sedan beräknas dubbelintegralen med formeln
, sedan beräknas dubbelintegralen med formeln
 .
.
Exempel 1.3. Beräkna arean av figuren avgränsad av dessa linjer:  ,
, ,
, ,
, .
.
Lösning. För att beräkna arean av ett område  Låt oss använda formeln:
Låt oss använda formeln:  .
.
|
|
Låt oss skildra området ,
,
Låt oss gå vidare till polära koordinater:
I det polära koordinatsystemet, området |





 .
.
1.2. Trippelintegraler
De grundläggande egenskaperna hos trippelintegraler liknar egenskaperna hos dubbla integraler.
I kartesiska koordinater skrivs trippelintegralen vanligtvis på följande sätt:
 .
.
Om  , sedan trippelintegralen över området
, sedan trippelintegralen över området  numeriskt lika med kroppens volym
numeriskt lika med kroppens volym  :
:
 .
.
Trippelintegralberäkning
Låt domänen av integration  begränsas under respektive ovanför av envärdiga sammanhängande ytor
begränsas under respektive ovanför av envärdiga sammanhängande ytor  ,
, och projiceringen av regionen
och projiceringen av regionen  till koordinatplanet
till koordinatplanet  det finns ett platt område
det finns ett platt område  (Fig. 1.6).
(Fig. 1.6).
|
|
Sedan för fasta värden Då får vi:
Om dessutom projektionen
Var |
 .
.
Exempel 1.4. Beräkna  , Var
, Var  - en kropp begränsad av flygplan:
- en kropp begränsad av flygplan:
|
|
Lösning. Integrationsområdet är en pyramid (fig. 1.7). Projektionsområde
|
|
|
Att sätta gränserna för integration för en triangel
|
Trippelintegral i cylindriska koordinater
När man flyttar från kartesiska koordinater  till cylindriska koordinater
till cylindriska koordinater  (Fig. 1.9) i samband med
(Fig. 1.9) i samband med  relationer
relationer  ,
, ,
, , och
, och
|
|
trippelintegralen omvandlas: Exempel 1.5. Beräkna volymen av en kropp avgränsad av ytor: Lösning. Erforderlig kroppsvolym |
|
|
Integreringsdomänen är en del av en cylinder som avgränsas nedanför av ett plan Låt oss gå vidare till cylindriska koordinater.
eller i cylindriska koordinater: |
Område  , avgränsad av en kurva
, avgränsad av en kurva  , kommer att ta formen, eller
, kommer att ta formen, eller  , medan den polära vinkeln
, medan den polära vinkeln
 . Som ett resultat har vi
. Som ett resultat har vi

 .
.
2. Element av fältteori
Låt oss först komma ihåg metoderna för att beräkna kurvlinjära och ytintegraler.
Beräkning av en kurvlinjär integral över koordinater för funktioner definierade på en kurva  , reducerar till att beräkna en bestämd integral av formen
, reducerar till att beräkna en bestämd integral av formen
om kurvan  specificeras parametriskt
specificeras parametriskt  motsvarar kurvans startpunkt
motsvarar kurvans startpunkt  , A
, A  - dess slutpunkt.
- dess slutpunkt.
Beräkning av ytintegralen för en funktion  , definierad på en tvåsidig yta
, definierad på en tvåsidig yta  , handlar om att beräkna en dubbelintegral, till exempel av formen
, handlar om att beräkna en dubbelintegral, till exempel av formen
|
|
om ytan  , ges av ekvationen
, ges av ekvationen  , projiceras unikt på planet
, projiceras unikt på planet  till regionen
till regionen  . Här
. Här  - vinkel mellan enhetsnormalvektor
- vinkel mellan enhetsnormalvektor  till ytan
till ytan  och axel
och axel  :
:
|
|
Sidan av ytan som krävs av problemförhållandena  bestäms av valet av lämpligt tecken i formel (2.3).
bestäms av valet av lämpligt tecken i formel (2.3).
Definition 2.1. Vektor fält
 kallas vektorfunktionen för en punkt
kallas vektorfunktionen för en punkt  tillsammans med dess omfattning:
tillsammans med dess omfattning:
Vektor fält  kännetecknas av en skalär kvantitet – divergens:
kännetecknas av en skalär kvantitet – divergens:
Definition 2.2. Flöde
vektor fält
 genom ytan
genom ytan
 kallas ytintegralen:
kallas ytintegralen:
|
|
Var  - enhetsnormalvektor till den valda sidan av ytan
- enhetsnormalvektor till den valda sidan av ytan  , A
, A  - skalär produkt av vektorer
- skalär produkt av vektorer  Och
Och  .
.
Definition 2.3. Omlopp vektor fält
Förbi
stängd kurva  kallas en krökt integral
kallas en krökt integral
|
|
Var  .
.
Ostrogradsky-Gauss formel
upprättar en koppling mellan vektorfältflödet
 genom en sluten yta
genom en sluten yta
 och fältdivergens:
och fältdivergens:
Var
 - yta avgränsad av en sluten kontur
- yta avgränsad av en sluten kontur
 , A
, A
 är enhetens normalvektor till denna yta. Normalens riktning måste överensstämma med konturens riktning
är enhetens normalvektor till denna yta. Normalens riktning måste överensstämma med konturens riktning
 .
.
Exempel 2.1. Beräkna ytintegralen
 ,
,
Var  - yttre delen av konen
- yttre delen av konen  (
( ), avskuren av ett flygplan
), avskuren av ett flygplan  (Figur 2.1).
(Figur 2.1).
Lösning. Yta  unikt projiceras in i regionen
unikt projiceras in i regionen  plan
plan  , och integralen beräknas med formeln (2.2).
, och integralen beräknas med formeln (2.2).
|
|
Enhetsyta normalvektor
Här, i uttrycket för normalen, väljs plustecknet, eftersom vinkeln |
Område  det finns en cirkel
det finns en cirkel  . Därför går vi i den sista integralen till polära koordinater, medan
. Därför går vi i den sista integralen till polära koordinater, medan  ,
, :
:
Exempel 2.2. Hitta divergensen och krullen för ett vektorfält  .
.
Lösning. Med hjälp av formel (2.4) får vi
Rotorn för ett givet vektorfält hittas med formeln (2.5)

Exempel 2.3. Hitta flödet av ett vektorfält  genom en del av planet
genom en del av planet  :
: , belägen i den första oktanten (normalen bildar en spetsig vinkel med axeln
, belägen i den första oktanten (normalen bildar en spetsig vinkel med axeln  ).
).
|
|
Lösning. Med hjälp av formel (2.6)
Låt oss avbilda en del av planet
(Fig. 2.3). Normalvektorn till planet har koordinater: |
|
|
|
Var  - planprojektion
- planprojektion  på
på  (Fig. 2.4).
(Fig. 2.4).
Exempel 2.4. Beräkna flödet av ett vektorfält genom en sluten yta  , bildad av planet
, bildad av planet  och en del av konen
och en del av konen  (
( ) (Fig. 2.2).
) (Fig. 2.2).
Lösning. Låt oss använda Ostrogradsky-Gauss formel (2.8)
 .
.
Låt oss hitta divergensen för vektorfältet  enligt formel (2.4):
enligt formel (2.4):
Var  är volymen av konen över vilken integrationen utförs. Låt oss använda den välkända formeln för att beräkna volymen av en kon
är volymen av konen över vilken integrationen utförs. Låt oss använda den välkända formeln för att beräkna volymen av en kon  (
( - radien för konens bas,
- radien för konens bas,  - hans höga). I vårt fall får vi
- hans höga). I vårt fall får vi  . Äntligen får vi
. Äntligen får vi
 .
.
Exempel 2.5. Beräkna cirkulationen av ett vektorfält  längs konturen
längs konturen
 , bildad av skärningspunkten mellan ytor
, bildad av skärningspunkten mellan ytor  Och
Och  (
( ). Kontrollera resultatet med Stokes formel.
). Kontrollera resultatet med Stokes formel.
Lösning. Skärningspunkten mellan dessa ytor är en cirkel  ,
, (Fig. 2.1). Traverseringsriktningen väljs vanligtvis så att området som begränsas av den förblir till vänster. Låt oss skriva de parametriska ekvationerna för konturen
(Fig. 2.1). Traverseringsriktningen väljs vanligtvis så att området som begränsas av den förblir till vänster. Låt oss skriva de parametriska ekvationerna för konturen
 :
:
|
|
och parametern  varierar från
varierar från  innan
innan  . Med hjälp av formel (2.7), med hänsyn till (2.1) och (2.10), får vi
. Med hjälp av formel (2.7), med hänsyn till (2.1) och (2.10), får vi
 .
.
Låt oss nu tillämpa Stokes formel (2.9). Som en yta  , sträckt på konturen
, sträckt på konturen
 , kan du ta del av planet
, kan du ta del av planet  . Normal riktning
. Normal riktning  till denna yta överensstämmer med konturens riktning
till denna yta överensstämmer med konturens riktning
 . Krullen för ett givet vektorfält beräknas i exempel 2.2:
. Krullen för ett givet vektorfält beräknas i exempel 2.2:  . Därför önskad cirkulation
. Därför önskad cirkulation
Var  - området i regionen
- området i regionen  .
. - cirkelradie
- cirkelradie  , var
, var
Låt oss ha två rektangulära koordinatsystem i rymden och  och ett system av funktioner
och ett system av funktioner
 (1)
(1)
som upprättar en en-till-en-överensstämmelse mellan punkter i vissa områden  Och
Och  i dessa koordinatsystem. Låt oss anta att funktionerna i system (1) har
i dessa koordinatsystem. Låt oss anta att funktionerna i system (1) har  kontinuerliga partiella derivator. Determinanten som består av dessa partiella derivator
kontinuerliga partiella derivator. Determinanten som består av dessa partiella derivator
 ,
,
kallas den jakobiska (eller jakobiska determinanten) för funktionssystemet (1). Vi kommer att anta det  V
V  .
.
Under de antaganden som gjorts ovan gäller följande allmänna formel för att ändra variabler i en trippelintegral:

Som i fallet med dubbelintegralen, den ömsesidiga unikheten hos systemet (1) och tillståndet  kan kränkas på enskilda punkter, på enskilda linjer och på enskilda ytor.
kan kränkas på enskilda punkter, på enskilda linjer och på enskilda ytor.
System av funktioner (1) för varje punkt  matchar en enda poäng
matchar en enda poäng  . Dessa tre siffror
. Dessa tre siffror  kallas kurvlinjära koordinater för en punkt
kallas kurvlinjära koordinater för en punkt  . Punkter i rymden
. Punkter i rymden  , för vilken en av dessa koordinater bibehåller ett konstant värde, bildar den s.k. koordinatyta.
, för vilken en av dessa koordinater bibehåller ett konstant värde, bildar den s.k. koordinatyta.
II Trippelintegral i cylindriska koordinater
Det cylindriska koordinatsystemet (CSS) bestäms av planet  , där ett polärt koordinatsystem specificeras och axeln
, där ett polärt koordinatsystem specificeras och axeln  , vinkelrätt mot detta plan. Cylindriska koordinater för en punkt
, vinkelrätt mot detta plan. Cylindriska koordinater för en punkt 
 , Var
, Var  – punktens polära koordinater
– punktens polära koordinater  – projektioner t
– projektioner t  glasögon
glasögon  till planet
till planet  , A
, A  – dessa är koordinaterna för projektionen av punkten
– dessa är koordinaterna för projektionen av punkten  per axel
per axel  eller
eller  .
.
I plan  vi anger kartesiska koordinater på vanligt sätt, rikta applikataxeln längs axeln
vi anger kartesiska koordinater på vanligt sätt, rikta applikataxeln längs axeln  CSK. Nu är det inte svårt att få formler som förbinder cylindriska koordinater med kartesiska:
CSK. Nu är det inte svårt att få formler som förbinder cylindriska koordinater med kartesiska:
 (3)
(3)
Dessa formler mappar området till hela utrymmet  .
.
Koordinatytorna i det aktuella fallet kommer att vara:
1)
 – cylindriska ytor med generatriser parallella med axeln
– cylindriska ytor med generatriser parallella med axeln  , vars guider är cirklar i planet
, vars guider är cirklar i planet  , centrerad på punkten
, centrerad på punkten  ;
;
2)

 ;
;
3)
 – plan parallella med planet
– plan parallella med planet  .
.
Jacobian av systemet (3):
 .
.
Den allmänna formeln för CSK har följande form:
Anteckning 1
.
Övergången till cylindriska koordinater rekommenderas i det fall när integrationsområdet är en cirkulär cylinder eller kon, eller en rotationsparaboloid (eller delar därav), och axeln för denna kropp sammanfaller med applikationens axel  .
.
Anteckning 2. Cylindriska koordinater kan generaliseras på samma sätt som polära koordinater i ett plan.
Exempel 1. Beräkna trippelintegralen för en funktion

efter region  , representerar den inre delen av cylindern
, representerar den inre delen av cylindern  , avgränsad av en kon
, avgränsad av en kon  och paraboloid
och paraboloid  .
.
Lösning. Vi har redan övervägt detta område i §2, exempel 6, och fått en standardpost i DPSC. Det är dock svårt att beräkna integralen i denna region. Låt oss gå till CSK:
 .
.
Utsprång  kropp
kropp  till planet
till planet  - det är en cirkel
- det är en cirkel  . Därför koordinaten
. Därför koordinaten  varierar från 0 till
varierar från 0 till  , A
, A  – från 0 till R.
Genom en godtycklig punkt
– från 0 till R.
Genom en godtycklig punkt  dra en rät linje parallellt med axeln
dra en rät linje parallellt med axeln  . Den raka linjen kommer att gå in
. Den raka linjen kommer att gå in  på en kon, men kommer ut på en paraboloid. Men konen
på en kon, men kommer ut på en paraboloid. Men konen  har ekvationen i CSC
har ekvationen i CSC  och paraboloiden
och paraboloiden  - ekvationen
- ekvationen  . Så vi har
. Så vi har
III Trippelintegral i sfäriska koordinater
Det sfäriska koordinatsystemet (SCS) bestäms av planet  , där UCS specificeras, och axeln
, där UCS specificeras, och axeln  , vinkelrätt mot planet
, vinkelrätt mot planet  .
.
Sfäriska koordinater för en punkt  rymden kallas en trippel av tal
rymden kallas en trippel av tal  , Var
, Var  – polär projektionsvinkel för en punkt på ett plan
– polär projektionsvinkel för en punkt på ett plan  ,
, – vinkel mellan axel
– vinkel mellan axel  och vektor
och vektor  Och
Och  .
.
I plan  låt oss introducera kartesiska koordinataxlar
låt oss introducera kartesiska koordinataxlar  Och
Och  på vanligt sätt, och applikationsaxeln är kompatibel med axeln
på vanligt sätt, och applikationsaxeln är kompatibel med axeln  . Formlerna som förbinder sfäriska koordinater med kartesiska är följande:
. Formlerna som förbinder sfäriska koordinater med kartesiska är följande:
 (4)
(4)
Dessa formler mappar området till hela utrymmet  .
.
Jacobian av funktionssystemet (4):
 .
.
Det finns tre familjer av koordinatytor:
1)
 – koncentriska sfärer med centrum i origo;
– koncentriska sfärer med centrum i origo;
2)
 – halvplan som passerar genom axeln
– halvplan som passerar genom axeln  ;
;
3)
 – cirkulära koner med en vertex i utgångspunkten för koordinaterna, vars axel är axeln
– cirkulära koner med en vertex i utgångspunkten för koordinaterna, vars axel är axeln  .
.
Formel för övergång till SSC i trippelintegral:

Anmärkning 3.
Övergången till SCS rekommenderas när integrationsdomänen är en boll eller en del av den. I det här fallet sfärens ekvation  går in i. Liksom CSK som diskuterades tidigare är CSK "bunden" till axeln
går in i. Liksom CSK som diskuterades tidigare är CSK "bunden" till axeln  . Om sfärens centrum förskjuts med en radie längs koordinataxeln, får vi den enklaste sfäriska ekvationen när den förskjuts längs axeln
. Om sfärens centrum förskjuts med en radie längs koordinataxeln, får vi den enklaste sfäriska ekvationen när den förskjuts längs axeln  :
:
Anmärkning 4. Det är möjligt att generalisera SSC:

med Jacobian  . Detta system av funktioner kommer att översätta ellipsoiden
. Detta system av funktioner kommer att översätta ellipsoiden

att "parallellepiped"
Exempel 2.
Hitta det genomsnittliga avståndet för punkter på en boll med radie  från dess centrum.
från dess centrum.
Lösning.
Kom ihåg att det genomsnittliga värdet av funktionen  i området
i området  är trippelintegralen av en funktion över en region dividerad med regionens volym. I vårat fall
är trippelintegralen av en funktion över en region dividerad med regionens volym. I vårat fall
Så vi har

Trippelintegraler. Beräkning av kroppsvolym.
Trippelintegral i cylindriska koordinater
I tre dagar låg den döde på prostens kontor, klädd i Pythagoras byxor,
I händerna på Fichtenholtz höll han en volym som hade fört honom från denna värld,
En trippelintegral knöts till benen, och liket lindades in i en matris,
Och istället för att be, läste någon oförskämd person Bernoullis teorem.
Trippelintegraler är något du inte behöver vara rädd för =) För om du läser den här texten har du med största sannolikhet en god förståelse för teori och praktik av "vanliga" integraler, och dubbla integraler. Och där det finns en dubbel, i närheten finns en trippel:
![]()
Och egentligen, vad finns det att frukta? Integralen är mindre, integralen är mer....
Låt oss titta på inspelningen:
– trippel integrerad ikon;
– integrand funktion av tre variabler;
– produkt av differentialer.
– integrationsområde.
Låt oss särskilt fokusera på integrationsområden. Om i dubbel integral det representerar platt figur, då här – rumslig kropp, som, som bekant, begränsas av uppsättningen ytor. Utöver ovanstående måste du alltså navigera rymdens grundläggande ytor och kunna göra enkla tredimensionella ritningar.
Vissa är deprimerade, jag förstår... Tyvärr kan artikeln inte heta "trippelintegraler för dummies", och det finns några saker du behöver veta/kunna göra. Men det är okej - allt material presenteras i en extremt tillgänglig form och kan bemästras på kortast möjliga tid!
Vad innebär det att beräkna en trippelintegral och vad är den jämn?
Att beräkna trippelintegralen betyder hitta NUMMER:
I det enklaste fallet, när trippelintegralen är numeriskt lika med kroppens volym. Och faktiskt, enligt allmänna innebörden av integration, produkten är lika oändligt liten volymen av en elementär "tegelsten" av kroppen. Och trippelintegralen är rättvis förenar
alla dessa oändligt små partiklaröver området, vilket resulterar i det integrerade (totala) värdet av kroppens volym: ![]() .
.
Dessutom har trippelintegralen viktig fysiska applikationer. Men mer om detta senare - i den andra delen av lektionen, tillägnad beräkningar av godtyckliga trippelintegraler, för vilken funktionen i det allmänna fallet skiljer sig från en konstant och är kontinuerlig i regionen. I den här artikeln kommer vi att i detalj överväga problemet med att hitta volym, som enligt min subjektiva bedömning förekommer 6-7 gånger oftare.
Hur löser man en trippelintegral?
Svaret följer logiskt av föregående stycke. Behöver bestämma kroppsövergångsordning och gå till itererade integraler. Ta sedan hand om tre enkla integraler sekventiellt.
Som ni ser påminner hela köket väldigt, väldigt mycket dubbla integraler, med skillnaden att nu har vi lagt till ytterligare en dimension (i stort sett höjd). Och förmodligen har många av er redan gissat hur trippelintegraler löses.
Låt oss skingra alla återstående tvivel:
Exempel 1
Skriv ner i en kolumn på papper:
Och svara på följande frågor. Vet du vilka ytor som definierar dessa ekvationer? Förstår du den informella innebörden av dessa ekvationer? Kan du föreställa dig hur dessa ytor ligger i rymden?
Om du är benägen till det allmänna svaret "snarare nej än ja", var noga med att arbeta igenom lektionen, annars kommer du inte vidare!
Lösning: vi använder formeln.
För att ta reda på det kroppsövergångsordning och gå till itererade integraler du behöver (allt genialt är enkelt) för att förstå vilken typ av kropp detta är. Och i många fall bidrar teckningar i hög grad till sådan förståelse.
Av tillstånd begränsas kroppen av flera ytor. Var ska man börja bygga? Jag föreslår följande procedur:
Låt oss först skildra parallella ortogonala projicering av kroppen på koordinatplanet. Första gången jag sa vad den här projektionen heter, lol =)
Eftersom projektion utförs längs axeln, är det först och främst tillrådligt att ta itu med ytor, som är parallella med denna axel. Låt mig påminna dig om att ekvationerna för sådana ytor innehåller inte bokstaven "z". Det finns tre av dem i det aktuella problemet:
– ekvationen anger ett koordinatplan som passerar genom axeln;
– ekvationen anger ett koordinatplan som passerar genom axeln;
– ekvationen sätts plan "platt" rak linje parallellt med axeln.
Troligtvis är den önskade projektionen följande triangel: 
Kanske inte alla helt förstod vad vi pratade om. Föreställ dig att en axel kommer ut från skärmen och sticker direkt in i näsryggen ( de där. det visar sig att du tittar på en 3-dimensionell ritning från ovan). Den rumsliga kroppen som studeras är belägen i en ändlös trihedrisk "korridor" och dess projektion på ett plan representerar sannolikt en skuggad triangel.
Jag skulle vilja fästa särskild uppmärksamhet på det faktum att medan vi har uttryckt bara ett antagande om projektion och klausulerna "mest troligt" och "mest troligt" var inte slumpmässiga. Faktum är att inte alla ytor har analyserats ännu och det kan hända att en av dem "hakar av" en del av triangeln. Som ett tydligt exempel antyder detta sfär med ett centrum vid utgångspunkten för en radie som är mindre än en, till exempel en sfär ![]() – dess projektion på planet (cirkel
– dess projektion på planet (cirkel ![]() ) kommer inte att helt "täcka" det skuggade området, och den slutliga projektionen av kroppen kommer inte att vara en triangel alls (cirkeln kommer att "klippa av" sina skarpa hörn).
) kommer inte att helt "täcka" det skuggade området, och den slutliga projektionen av kroppen kommer inte att vara en triangel alls (cirkeln kommer att "klippa av" sina skarpa hörn).
I det andra steget tar vi reda på hur kroppen begränsas uppifrån och underifrån och utför en rumslig ritning. Låt oss återgå till problemformuleringen och se vilka ytor som finns kvar. Ekvationen anger själva koordinatplanet och ekvationen – parabolisk cylinder, belägen ovan plan och passerar genom axeln. Således är projektionen av kroppen verkligen en triangel.
Förresten, jag hittade den här redundans förhållanden - det var inte nödvändigt att inkludera planets ekvation, eftersom ytan, som rör vid abskissaxeln, redan stänger kroppen. Det är intressant att notera att i det här fallet skulle vi inte omedelbart kunna rita projektionen - triangeln skulle "rita" först efter att ha analyserat ekvationen.
Låt oss noggrant avbilda ett fragment av en parabolcylinder: 
Efter att ha färdigställt ritningarna med ordningen att gå runt kroppen inga problem!
Först bestämmer vi ordningen för övergången av projektionen (samtidigt är det MYCKET BEKVÄMARE att navigera med hjälp av en tvådimensionell ritning). Det är gjort EXAKT SAMMA, Som i dubbla integraler! Tänk på en laserpekare och skanna ett plant område. Låt oss välja den "traditionella" 1:a bypassmetoden:
Därefter tar vi upp en trolllykta, tittar på den tredimensionella ritningen och strikt från botten till toppen Vi belyser patienten. Strålar kommer in i kroppen genom ett plan och går ut genom ytan. Således är ordningen för att korsa kroppen:
Låt oss gå vidare till upprepade integraler: 
1) Du bör börja med "zeta"-integralen. Vi använder Newton-Leibniz formel:
Låt oss ersätta resultatet med "spel"-integralen: 
Vad hände? I huvudsak reducerades lösningen till en dubbel integral och exakt till formeln ![]() volym av cylindrisk balk! Det som följer är bekant:
volym av cylindrisk balk! Det som följer är bekant:
2) 
Var uppmärksam på den rationella tekniken för att lösa den 3:e integralen.
Svar: ![]()
Beräkningar kan alltid skrivas på "en rad": 
Men var försiktig med den här metoden - att öka hastigheten är fylld med kvalitetsförlust, och ju mer komplext exemplet är, desto större är chansen att göra ett misstag.
Låt oss svara på en viktig fråga:
Är det nödvändigt att göra ritningar om uppgiftsförhållandena inte kräver att de implementeras?
Du kan gå på fyra sätt:
1) Rita projektionen och själva kroppen. Detta är det mest fördelaktiga alternativet - om du har möjlighet att slutföra två anständiga ritningar, var inte lat, gör båda ritningarna. Jag rekommenderar det först.
2) Rita bara kroppen. Lämplig när kroppen har en enkel och tydlig projektion. Så, till exempel, i det demonterade exemplet skulle en tredimensionell ritning vara tillräckligt. Men det finns också ett minus - det är obekvämt att bestämma ordningen för att korsa projektionen från en 3D-bild, och jag skulle rekommendera den här metoden endast till personer med en bra utbildningsnivå.
3) Rita bara projektionen. Detta är inte heller dåligt, men då krävs ytterligare skriftliga kommentarer vilket begränsar området från olika håll. Tyvärr tvingas det tredje alternativet ofta - när kroppen är för stor eller dess konstruktion är fylld med andra svårigheter. Och vi kommer också att överväga sådana exempel.
4) Gör helt utan ritningar. I det här fallet måste du föreställa dig kroppen mentalt och kommentera dess form/placering skriftligt. Lämplig för mycket enkla kroppar eller uppgifter där det är svårt att utföra båda ritningarna. Men det är fortfarande bättre att göra åtminstone en schematisk ritning, eftersom en "naken" lösning kan avvisas.
Följande organ är för självständigt arbete:
Exempel 2
Med hjälp av en trippelintegral, beräkna volymen av en kropp avgränsad av ytor
I det här fallet specificeras integrationsdomänen främst av ojämlikheter, och detta är ännu bättre - en uppsättning ojämlikheter ![]() definierar 1:a oktanten, inklusive koordinatplan, och ojämlikheten – halva utrymmet, som innehåller ursprunget (kolla upp)+ själva planet. Det "vertikala" planet skär paraboloiden längs parabeln, och det är tillrådligt att konstruera detta avsnitt på ritningen. För att göra detta måste du hitta en ytterligare referenspunkt, det enklaste sättet är parabelns vertex (vi tar hänsyn till värdena
definierar 1:a oktanten, inklusive koordinatplan, och ojämlikheten – halva utrymmet, som innehåller ursprunget (kolla upp)+ själva planet. Det "vertikala" planet skär paraboloiden längs parabeln, och det är tillrådligt att konstruera detta avsnitt på ritningen. För att göra detta måste du hitta en ytterligare referenspunkt, det enklaste sättet är parabelns vertex (vi tar hänsyn till värdena ![]() och beräkna motsvarande "zet").
och beräkna motsvarande "zet").
Låt oss fortsätta att värma upp:
Exempel 3
Med hjälp av en trippelintegral, beräkna volymen av kroppen som avgränsas av de angivna ytorna. Utför ritningen.
Lösning: Formuleringen "utför en ritning" ger oss en viss frihet, men antyder troligen utförandet av en rumslig ritning. Projicering kommer dock inte att skada heller, särskilt eftersom det inte är det enklaste här.
Vi håller oss till den tidigare beprövade taktiken - först ska vi ta itu med ytor, som är parallella med applikationsaxeln. Ekvationerna för sådana ytor innehåller inte uttryckligen variabeln "z":
– ekvationen anger koordinatplanet som går genom axeln ( som på planet bestäms av den "eponyma" ekvationen);
– ekvationen sätts plan, passerar genom "eponymt" "platt" rak linje parallellt med axeln.
Den önskade kroppen begränsas av ett plan under och parabolisk cylinder ovan: 
Låt oss skapa en ordning för korsning av kroppen, medan "X" och "Y" gränserna för integration, jag påminner dig, är det bekvämare att ta reda på det med en tvådimensionell ritning:
Således: 
1) 
När man integrerar över "y" anses "x" vara en konstant, så det är lämpligt att omedelbart ta konstanten ur integraltecknet.
3) 
Svar:
Ja, jag glömde nästan, i de flesta fall är det till liten nytta (och till och med skadligt) att kontrollera resultatet som erhålls med en tredimensionell ritning, eftersom det med stor sannolikhet volym illusion, som jag pratade om i klassen Volymen av en revolutionskropp. Så när jag utvärderade problemets kropp, verkade det för mig personligen som att det hade mycket mer än 4 "kuber".
Följande exempel för en oberoende lösning:
Exempel 4
Med hjälp av en trippelintegral, beräkna volymen av kroppen som avgränsas av de angivna ytorna. Gör ritningar av denna kropp och dess projektion på ett plan.
Ett ungefärligt exempel på en uppgift i slutet av lektionen.
Det är inte ovanligt när det är svårt att utföra en tredimensionell ritning:
Exempel 5
Använd en trippelintegral och hitta volymen av en kropp som ges av dess gränsytor
Lösning: projektionen här är inte komplicerad, men du måste tänka på ordningen för att korsa den. Om du väljer den första metoden måste siffran delas upp i 2 delar, vilket allvarligt hotar att beräkna summan två trippelintegraler. I detta avseende ser den andra vägen mycket mer lovande ut. Låt oss uttrycka och skildra projektionen av denna kropp på ritningen: 
Jag ber om ursäkt för kvaliteten på några av bilderna, jag klippte dem direkt från mina egna manuskript.
Vi väljer en mer fördelaktig ordning för att korsa figuren: 
Nu är det upp till kroppen. Underifrån begränsas det av planet, från ovan - av planet som passerar genom ordinataaxeln. Och allt skulle vara bra, men det sista planet är för brant och att bygga området är inte så lätt. Valet här är föga avundsvärt: antingen smycken fungerar i liten skala (eftersom kroppen är ganska tunn), eller en ritning cirka 20 centimeter hög (och även då, om det passar).
Men det finns en tredje, inhemsk rysk metod för att lösa problemet - att göra poäng =) Och istället för en tredimensionell ritning, nöj dig med en verbal beskrivning: "Denna kropp är begränsad av cylindrar ![]() och ett plan från sidan, ett plan underifrån och ett plan ovanifrån.”
och ett plan från sidan, ett plan underifrån och ett plan ovanifrån.”
De "vertikala" gränserna för integration är uppenbarligen:
Låt oss beräkna kroppens volym och inte glömma att vi kringgick projektionen på ett mindre vanligt sätt: 
1) 
Svar:
Som du märkte är kroppar som föreslås i problem som inte är dyrare än hundra spänn ofta begränsade av planet nedan. Men detta är inte en regel, så du måste alltid vara på vakt - du kan stöta på en uppgift där kroppen befinner sig och under platt Så, till exempel, om vi i det analyserade problemet istället betraktar planet, så kommer den undersökta kroppen att kartläggas symmetriskt i det nedre halvrummet och begränsas av planet underifrån och av planet ovanifrån!
Det är lätt att se att du får samma resultat:
(kom ihåg att kroppen måste gå runt strikt från botten till toppen!)
Dessutom kan "favorit" planet inte användas alls; det enklaste exemplet: en boll som ligger ovanför planet - när man beräknar dess volym kommer en ekvation inte att behövas alls.
Vi kommer att överväga alla dessa fall, men för närvarande finns det en liknande uppgift för dig att lösa på egen hand:
Exempel 6
Använd trippelintegralen och hitta volymen av en kropp som begränsas av ytor ![]()
En kort lösning och svar i slutet av lektionen.
Låt oss gå vidare till andra stycket med lika populära material:
Trippelintegral i cylindriska koordinater
Cylindriska koordinater är i huvudsak polära koordinater i rymden.
I ett cylindriskt koordinatsystem bestäms positionen för en punkt i rymden av punktens polära koordinater - projektionen av punkten på planet och applikationen av själva punkten.
Övergången från ett tredimensionellt kartesiskt system till ett cylindriskt koordinatsystem utförs enligt följande formler: 
I relation till vårt ämne ser förvandlingen ut så här:
Och följaktligen i det förenklade fallet som vi överväger i den här artikeln: ![]()
Det viktigaste är att inte glömma den extra "er"-multiplikatorn och placera den korrekt polära gränser för integration när du korsar projektionen:
Exempel 7
Lösning: vi följer samma procedur: först och främst betraktar vi ekvationer där variabeln "ze" saknas. Det finns bara en här. Utsprång cylindrisk yta på planet representerar den "eponyma" cirkel .
Flygplan ![]() de begränsar den önskade kroppen underifrån och ovan ("klipp ut" den ur cylindern) och projicerar den i en cirkel:
de begränsar den önskade kroppen underifrån och ovan ("klipp ut" den ur cylindern) och projicerar den i en cirkel: 
Nästa upp är en tredimensionell ritning. Den största svårigheten ligger i att konstruera ett plan som skär cylindern i en "sned" vinkel, vilket resulterar i ellips. Låt oss förtydliga detta avsnitt analytiskt: för att göra detta skriver vi om planets ekvation i funktionell form ![]() och beräkna värdena för funktionen ("höjd") vid de uppenbara punkter som ligger på gränsen för projektionen:
och beräkna värdena för funktionen ("höjd") vid de uppenbara punkter som ligger på gränsen för projektionen:

Vi markerar de hittade punkterna på ritningen och noggrant (inte som jag =)) anslut dem med en linje: 
Projektionen av en kropp på ett plan är en cirkel, och detta är ett starkt argument för att flytta till ett cylindriskt koordinatsystem:
Låt oss hitta ekvationerna för ytor i cylindriska koordinater:
Nu måste du ta reda på ordningen för att korsa kroppen.
Låt oss först ta itu med projektion. Hur bestämmer man dess genomgångsordning? EXAKT SAMMA SOM MED beräkna dubbla integraler i polära koordinater. Här är det elementärt:
De "vertikala" gränserna för integration är också uppenbara - vi går in i kroppen genom planet och lämnar den genom planet:
![]()
Låt oss gå vidare till upprepade integraler: 
I det här fallet lägger vi omedelbart faktorn "er" i "vår" integral.
Som vanligt är en kvast lättare att bryta längs kvistarna:
1) 
Vi lägger resultatet i följande integral:
Och här glömmer vi inte att "phi" anses vara en konstant. Men detta är för tillfället:
Svar:
En liknande uppgift för dig att lösa på egen hand:
Exempel 8
Beräkna volymen av en kropp avgränsad av ytor med hjälp av en trippelintegral. Rita ritningar av denna kropp och dess projektion på ett plan.
Ett ungefärligt exempel på den slutliga designen i slutet av lektionen.
Observera att under villkoren för problemen sägs inte ett ord om övergången till ett cylindriskt koordinatsystem, och en okunnig person kommer att kämpa med svåra integraler i kartesiska koordinater. ...Eller kanske det inte gör det - trots allt finns det ett tredje, originellt ryskt sätt att lösa problem =)
Det är bara att börja! ...på ett bra sätt:=)
Exempel 9
Använd trippelintegralen och hitta volymen av en kropp som begränsas av ytor
Moderat och smakfullt.
Lösning: denna kropp är begränsad konisk yta Och elliptisk paraboloid. Läsare som noggrant har läst artikelmaterialet Grundläggande ytor av rymden, har redan föreställt mig hur kroppen ser ut, men i praktiken finns det ofta mer komplexa fall, så jag kommer att genomföra ett detaljerat analytiskt resonemang.
Först hittar vi linjerna längs vilka ytorna skär varandra. Låt oss komponera och lösa följande system:
Från den första ekvationen subtraherar vi den andra termen för term:
Resultatet är två rötter:
Låt oss ersätta det hittade värdet i valfri ekvation i systemet:
, varav det följer att
Således motsvarar roten en enda punkt - ursprunget. Naturligtvis eftersom hörn på ytorna i fråga sammanfaller.
Låt oss nu ersätta den andra roten - också i valfri ekvation i systemet:
Vilken är den geometriska betydelsen av resultatet? "På höjden" (i planet) korsar paraboloiden och konen cirkel– enhetsradie med centrum i punkt .
I det här fallet innehåller paraboloidens "skål" konens "tratt", därför formning Den koniska ytan ska ritas med en prickad linje (förutom segmentet av generatrisen längst bort från oss, som är synligt från denna vinkel):
Projektionen av en kropp på ett plan är cirkel med ett centrum i början av radie 1, som jag inte ens brydde mig om att avbilda på grund av det uppenbara i detta faktum (Däremot ger vi en skriftlig kommentar!). Förresten, i de två föregående problemen kunde projektionsritningen också poängsättas, om inte för skicket.
När man flyttar till cylindriska koordinater med standardformler skrivs olikheten i sin enklaste form och det finns inga problem med ordningen för att korsa projektionen:
Låt oss hitta ekvationerna för ytor i ett cylindriskt koordinatsystem: ![]()
Eftersom problemet tar hänsyn till den övre delen av konen, uttrycker vi från ekvationen:
"Vi skannar kroppen" från botten till toppen. Ljusstrålar kommer in i den genom en elliptisk paraboloid och går ut genom en konisk yta. Således är den "vertikala" ordningen för att korsa kroppen:
Resten är en fråga om teknik: 
Svar: ![]()
Det är inte ovanligt att en kropp inte definieras av dess begränsande ytor, utan av många ojämlikheter:
Exempel 10
![]()
Jag förklarade den geometriska betydelsen av rumsliga ojämlikheter tillräckligt detaljerat i samma referensartikel - Grundläggande ytor av rymden och deras konstruktion.
Även om denna uppgift innehåller en parameter, tillåter den att utföra en exakt ritning som återspeglar kroppens grundläggande utseende. Fundera på hur man bygger. En kort lösning och svar finns i slutet av lektionen.
...ja, ett par uppgifter till? Jag funderade på att slutföra lektionen, men jag känner bara att du vill ha mer =)
Exempel 11
Med hjälp av en trippelintegral, beräkna volymen av en given kropp: ![]() , där är ett godtyckligt positivt tal.
, där är ett godtyckligt positivt tal.
Lösning: ojämlikhet ![]() definierar en boll med centrum vid utgångspunkten för radien och ojämlikheten
definierar en boll med centrum vid utgångspunkten för radien och ojämlikheten ![]() – "insidan" av en cirkulär cylinder med en symmetriaxel med radie . Således begränsas den önskade kroppen av en cirkulär cylinder på sidan och sfäriska segment som är symmetriska i förhållande till planet upptill och nedtill.
– "insidan" av en cirkulär cylinder med en symmetriaxel med radie . Således begränsas den önskade kroppen av en cirkulär cylinder på sidan och sfäriska segment som är symmetriska i förhållande till planet upptill och nedtill.
Med detta som basmåttet, låt oss rita: 
Mer exakt borde det kallas en ritning, eftersom jag inte bibehöll proportionerna längs axeln särskilt bra. Men för att vara rättvis så krävde inte skicket någonting alls, och en sådan illustration visade sig vara helt tillräcklig.
Observera att här är det inte nödvändigt att ta reda på höjden vid vilken cylindern skär ut "locken" från bollen - om du tar en kompass i dina händer och använder den för att markera en cirkel med ett centrum vid radiens utgångspunkt 2 cm, då kommer skärningspunkterna med cylindern att dyka upp av sig själva.
Trippelintegralen skrivs så här:
Beräkna trippelintegral - betyder att hitta ett tal lika med kroppens volym V eller, vad är samma - områden V .
Nästan alla kan förstå innebörden av att beräkna en trippelintegral "den hårda vägen". Mer exakt - "under huden", och ännu mer exakt - i dess andningsorgan - lungorna. Oavsett om du vet det eller inte, finns det över 700 miljoner alveoler i människans lungor - vesikulära formationer sammanflätade med ett nätverk av kapillärer. Gasutbyte sker genom alveolernas väggar. Därför kan vi resonera så här: volymen gas i lungorna kan representeras som ett kompakt område. Och denna volym består av små volymer koncentrerade i alveolerna. Nyckelrollen i denna jämförelse spelas av det enorma antalet alveoler i lungorna: som vi kommer att se i nästa stycke, genom ett sådant "stort antal små saker" formuleras begreppet en trippelintegral matematiskt.
Varför används trippelintegralen för att hitta en kropps volym? V? Låt området V delat i n godtyckliga områden Δ vi, och denna beteckning betyder inte bara varje litet område, utan också dess volym. I varje sådant litet område väljs en godtycklig punkt Mi, A f(Mi)- funktionsvärde f(M) vid denna tidpunkt. Nu ska vi maximera antalet sådana små ytor och den största diametern Δ vi– tvärtom, minska. Vi kan komponera en integral summa av formen
Om funktionen f(M) = f(x, y, z) är kontinuerlig kommer den att existera integral summagräns den typ som anges ovan. Denna gräns kallas trippelintegral .
I det här fallet funktionen f(M) = f(x, y, z) kallas domänintegrerbar V ; V- område för integration; x, y, z- integrationsvariabler, dv(eller dx dy dz ) - volymelement.
Beräkning av trippelintegralen genom att reducera multipliciteten
Liksom i fallet med dubbla integraler, reduceras beräkningen av trippelintegraler till beräkningen av integraler med lägre multiplicitet.
Tänk på en tredimensionell region V. Under och ovanför (det vill säga i höjdled) begränsas detta område av ytor z = z1 (x, y) Och z = z2 (x, y) . På sidorna (det vill säga i bredd) begränsas området av ytor y = y1 (x) Och y = y2 (x) . Och slutligen, på djupet (om du tittar på området i axelns riktning Oxe) - ytor x = a Och x = b
För att tillämpa övergången till integraler med lägre multiplicitet, krävs det att den tredimensionella domänen V var korrekt. Det är korrekt när linjen är parallell med axeln Uns, korsar regiongränsen V på högst två punkter. Regelbundna tredimensionella regioner är till exempel en kuboid, en ellipsoid och en tetraeder. Figuren nedan visar en rektangulär parallellepiped, som vi kommer att möta i det första problemlösningsexemplet.

För att visualisera skillnaden mellan korrekthet och felaktighet lägger vi till att regionens ytor längs med den korrekta regionens höjd inte ska vara konkava inåt. Bilden nedan är ett exempel på ett felaktigt område V- en enkelarkshyperboloid, vars yta är rak, parallell med axeln Uns(röd), skär i mer än två punkter.

Vi kommer bara att överväga de korrekta områdena.
Alltså området V- korrekt. Sedan för vilken funktion som helst f(x, y, z) , kontinuerligt i regionen V, formeln är giltig

Denna formel låter dig reducera beräkningen av trippelintegralen till sekventiell beräkning av den interna bestämda integralen över variabeln z(vid konstant x Och y) och den yttre dubbelintegralen över en tvådimensionell domän D .
Genom att gå från dubbelintegralen till den upprepade får vi följande formel för att beräkna trippelintegralen:

För att beräkna en trippelintegral måste du alltså sekventiellt utvärdera tre bestämda integraler.
Dessa integraler beräknas från det innersta (över variabeln z) till den yttersta (genom variabel x). För att göra sekvensen av beräkningar lättare att förstå kan tre "kapslade" integraler skrivas enligt följande:
 .
.
Från det här inlägget är det redan klart att:
- först måste du integrera funktionen f(x, y, z) efter variabel z, och ta ekvationerna som integrationsgränser z = z1 (x, y) Och z = z2 (x, y) ytor som avgränsar området V under och över;
- y y = y1 (x) Och y = y2 (x) ytor som avgränsar området V från sidorna;
- integrera resultatet från föregående steg över variabeln x, och ta ekvationerna som integrationsgränser x = a Och x = b ytor som avgränsar området V grundlig.
Exempel 1. Låt oss gå från en trippelintegral till en itererad integral
![]() -
-
sekvenser av tre bestämda integraler. Utvärdera denna itererade integral.
Lösning. Beräkningen av den itererade integralen börjar alltid från den sista integralen:
![]() .
.
Låt oss beräkna den andra integralen - över variabeln y:
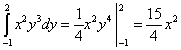 .
.
x:
 .
.
Svar: Denna upprepade integral och dess motsvarande trippelintegral är lika med 10.
Exempel 2. Beräkna trippelintegral
![]() ,
,
Var V- parallellepiped avgränsad av plan x = − 1 , x = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .
Lösning. Integrationsgränserna för alla tre bestämda integraler är unikt specificerade av ekvationerna för de ytor som avgränsar parallellepipeden. Därför reducerar vi omedelbart denna trippelintegral till en sekvens av tre bestämda integraler:
![]() .
.
z
 .
.
Vi beräknar integralen "i mitten" - över variabeln y. Vi får;
![]() .
.
Nu beräknar vi den yttersta integralen - över variabeln x:

Svar: Denna trippelintegral är -2.
Exempel 3. Beräkna trippelintegral
![]() ,
,
Var Vx + y + z = 1 och koordinera plan x = 0 , y = 0 , z= 0 . Område V projiceras på ett plan xOy till en triangel D, som visas i figuren nedan.

Lösning. Låt oss först sätta gränserna för integrationen. För integralen över en variabel z den nedre gränsen för integration är unikt specificerad: z= 0 . För att få den övre gränsen uttrycker vi z från x + y + z = 1 . Vi får 1- x − y. För integralen över en variabel y den nedre gränsen för integration är unikt specificerad: y= 0 . För att få den övre gränsen uttrycker vi y från x + y + z = 1 samtidigt som man överväger det z= 0 (eftersom linjen ligger i planet xOy). Vi får: 1 − x .
Vi reducerar denna trippelintegral till en sekvens av tre bestämda integraler:
 .
.
Vi beräknar den innersta integralen - över en variabel z, med tanke på x- och y-konstanter. Vi får:
 .
.
y. Vi får:

x:

Svar: Denna trippelintegral är lika med 1/8.
Beräkna trippelintegralen själv och titta sedan på lösningen
Exempel 4. Beräkna trippelintegral
![]() ,
,
Var V- en pyramid avgränsad av ett plan x + y + z = 1 och koordinera plan x = 0 , y = 0 , z = 0 .
Arrangemang av integrationsgränser vid övergång till en sekvens av tre integraler
Det händer att elever som inte har några speciella svårigheter att direkt räkna ut integraler inte kan vänja sig vid att sätta gränserna för integrationen när de går från en trippelintegral till en sekvens av tre bestämda integraler. Denna fråga kräver viss utbildning. I det första exemplet, integrationsdomänen V var en parallellepiped, med vilken allt är klart: den är avgränsad på alla sidor av plan, vilket betyder att integrationens gränser är unikt definierade av planens ekvationer. I det andra exemplet - en pyramid: här var det redan nödvändigt att tänka lite mer och uttrycka en av gränserna från ekvationen. Och om området V begränsas de av icke-plana ytor? Det är naturligtvis nödvändigt att besiktiga området på ett visst sätt V .
Låt oss börja med ett "mer fruktansvärt" exempel för att känna "situationen nära strid".
Exempel 5. Ordna gränserna för integration när du går från en trippelintegral, där regionen V- ellipsoid
![]() .
.

Lösning. Låt mitten av ellipsoiden vara origo, som visas i figuren ovan. Låt oss titta på ellipsoiden underifrån. Den begränsas underifrån av en yta, som är den del av ellipsoidens yta som är belägen under planet xOy z och det resulterande uttrycket med ett minustecken kommer att vara den nedre gränsen för integration över variabeln z:
![]() .
.
Låt oss nu titta på ellipsoiden ovanifrån. Här begränsas den av en yta, som är den del av ellipsoidens yta som ligger ovanför axeln xOy. Därför måste vi uttrycka från ellipsoidekvationen z och det resulterande uttrycket kommer att vara den övre gränsen för integration över variabeln z:
![]() .
.
Projektion av en ellipsoid på ett plan xOyär en ellipsoid. Hans ekvation:
För att få den nedre gränsen för integration över en variabel y, behöver uttryckas y från ellipsoidekvationen och ta det resulterande uttrycket med ett minustecken:
![]() .
.
För den övre gränsen för integration över en variabel y samma uttryck med ett plustecken:
Angående integration över en variabel x, sedan området V begränsat i djupet av flygplan. Därför gränserna för integration över en variabel x kan representeras som koordinaterna för områdets bakre och främre gränser. I fallet med en ellipsoid kommer de att vara värdena för halvaxellängderna tagna med negativa och positiva tecken a: x1 = − a Och x2 = a .
Således är sekvensen av integraler för att beräkna volymen av en ellipsoid som följer:
 ,
,
där "yrek first", "yrek second", "zet first" och "zet second" är uttrycken som erhållits ovan. Om du har lust och mod att beräkna denna integral och därmed volymen av ellipsoiden, så här är svaret: 4 πabc/3 .
Följande exempel är inte så skrämmande som det just diskuterade. Dessutom innebär de inte bara att sätta gränserna för integration, utan också att beräkna trippelintegralen själv. Testa vad du har lärt dig genom att följa lösningen på det skrämmande exemplet. Du måste fortfarande tänka när du sätter gränser.
Exempel 6. Beräkna trippelintegral
om integrationsdomänen är begränsad av plan x + y = 1 , x + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .
Lösning. Exemplet "resort" jämförs med exempel 5, eftersom gränserna för integration över "Y" och "Z" är unikt definierade. Men vi kommer att behöva hantera gränserna för integration över "X". Projektion av integrationsdomänen på planet xOyär en trapets ABCD.

I detta exempel är det mer fördelaktigt att projicera trapetsen på axeln Oj, annars, för att beräkna trippelintegralen, måste du dela upp figuren i tre delar. I exempel 4 började vi undersöka integrationsregionen underifrån, och detta är det vanliga förfarandet. Men i det här exemplet börjar vi inspektionen från sidan, eller, om det är lättare, lägger vi figuren på sidan och anser att vi tittar på den underifrån. Vi kan hitta gränserna för integration över "X" rent algebraiskt. För att göra detta uttrycker vi "x" från de första och andra ekvationerna som ges i exempelvillkoret. Från den första ekvationen får vi den nedre gränsen 1 − y, från den andra - övre 4 - 2 y. Låt oss reducera denna trippelintegral till en sekvens av tre bestämda integraler:
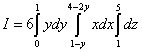 .
.
Uppmärksamhet! I det här exemplet är den yttersta integralen inte över variabeln "x", utan över variabeln "y", och den "genomsnittliga" integralen är över variabeln "x"! Här tillämpade vi en förändring av integrationsordningen, som vi blev bekanta med när vi studerade dubbelintegralen. Detta beror på det faktum att vi, som redan nämnts, började undersöka integrationsregionen inte underifrån, utan från sidan, det vill säga vi projicerade den inte på axeln Oxe, per axel Oj.
Vi beräknar den innersta integralen - över en variabel z, med tanke på x- och y-konstanter. Vi får:
Vi beräknar medelintegralen - över en variabel x. Vi får:
 .
.
Slutligen beräknar vi den yttersta integralen - över variabeln y:
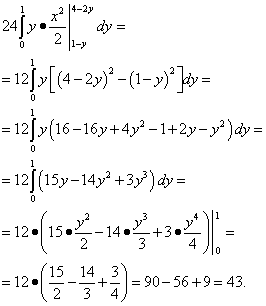
Svar: Denna trippelintegral är lika med 43.
Exempel 7. Beräkna trippelintegral
![]() ,
,
om integrationsområdet är begränsat till ytor x = 0 , y = 0 , z = 2 , x + y + z = 4 .
Lösning. Område V(pyramid MNRP) stämmer. Projektionsområde V till planet xOyär en triangel AOB.

De nedre gränserna för integration för alla variabler anges i exempelvillkoret. Låt oss hitta den övre gränsen för integration över "X". För att göra detta uttrycker vi "x" från den fjärde ekvationen, med tanke på "y" lika med noll och "ze" lika med två. Vi får x= 2 . Låt oss hitta den övre gränsen för integration över "spelet". För att göra detta, låt oss uttrycka "Y" från samma fjärde ekvation, med tanke på att "Z" är lika med två och "X" är ett variabelt värde. Vi får y = 2 − x. Och slutligen hittar vi den övre gränsen för integration över variabeln "z". För att göra detta, låt oss uttrycka "zet" från samma fjärde ekvation, och betrakta "y" och "zet" som variabla kvantiteter. Vi får z = 4 − x − y .
Låt oss reducera denna trippelintegral till en sekvens av tre bestämda integraler:
 .
.
Vi beräknar den innersta integralen - över en variabel z, med tanke på x- och y-konstanter. Vi får:
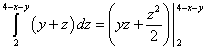 .
.
Vi beräknar medelintegralen - över en variabel y. Vi får:
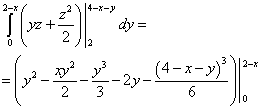 .
.
Vi beräknar den yttersta integralen - över en variabel x och slutligen finner vi denna trippelintegral:

Svar: Denna trippelintegral är lika med 2.
Förändring av variabler i trippelintegral och cylindriska koordinater
Om projektionen av integrationsdomänen på något av koordinatplanen är en cirkel eller del av en cirkel, så är trippelintegralen lättare att beräkna genom att övergå till cylindriska koordinater. Det cylindriska koordinatsystemet är en generalisering polärt koordinatsystem till rymden. I ett cylindriskt koordinatsystem, en punkt M kännetecknas av tre kvantiteter ( r, φ , z), Var r- avstånd från ursprunget till projektionen N poäng M till planet xOy, φ - vinkel mellan vektor PÅ och positiv axelriktning Oxe, z- appliceringspunkt M(bilden nedan).

Rektangulära koordinater x, y, z med cylindriska koordinater r, φ , z koppla formler
x = r cos φ ,
y = r synd φ ,
z = z .
För att flytta till cylindriska koordinater i en trippelintegral måste du uttrycka integranden som en funktion av variabler r, φ , z:
Det vill säga, övergången från rektangulära till cylindriska koordinater utförs enligt följande:
Trippelintegralen i cylindriska koordinater beräknas på samma sätt som i kartesiska rektangulära koordinater, genom att omvandla den till en sekvens av tre bestämda integraler:

Exempel 8. Beräkna trippelintegral
![]()
övergång till cylindriska koordinater, där V- område begränsat av ytor och.

Lösning. Sedan området V till planet xOy projiceras i en cirkel, sedan koordinaten φ varierar från 0 till 2 π , och koordinaten r- från r=0 till r=1. Ett konstant värde i rymden motsvarar en cylinder. Med tanke på skärningspunkten mellan denna cylinder och regionen V, får vi en förändring i ordinatan z från z = r upp till z= 1 . Låt oss gå vidare till cylindriska koordinater och få.
1. Cylindriska koordinater representerar kopplingen av polära koordinater i xy-planet med den vanliga kartesiska applikationen z (fig. 3).
Låt M(x, y, z) vara en godtycklig punkt i xyz-rymden, P vara projektionen av punkten M på xy-planet. Punkt M bestäms unikt av en trippel av tal - polära koordinater för punkt P, z - applikat av punkt M. Formler som förbinder dem med kartesiska har formen
Jacobian kartläggning (8)
Exempel 2.
Beräkna integral

där T är den yta som begränsas av ytor

Lösning. Låt oss flytta in integralen till sfäriska koordinater med hjälp av formler (9). Då kan integrationens domän specificeras av ojämlikheterna
Och det betyder

Exempel 3 Hitta kroppens volym begränsad av:
|
x 2 + y 2 + z 2 =8, |
Vi har: x 2 +y 2 +z 2 =8 - sfär med radie R= v8 med centrum i punkt O(000),
Den övre delen av konen z 2 =x 2 +y 2 med symmetriaxeln Oz och spetsen i punkt O (Fig. 2.20).
Låt oss hitta skärningslinjen mellan sfären och konen:

Och eftersom enligt villkoret z? 0 då

Cirkel R=2 som ligger i z=2-planet.

Därför, enligt (2.28)

där regionen U avgränsas ovanför
(en del av sfären),
(del av en kon);
region U projiceras på Oxy-planet in i region D - en cirkel med radie 2.
Därför är det tillrådligt att gå över till cylindriska koordinater i trippelintegralen med hjälp av formler (2.36):
Gränserna för förändring q, r finns i arean D v av hela cirkeln R = 2 med centrum i punkten O, därigenom: 0? q? 2р, 0? r? 2. Således ges regionen U i cylindriska koordinater av följande olikheter:

Lägg märke till att



Liknande artiklar


 (Fig. 1.5). För att göra detta omvandlar vi kurvorna:
(Fig. 1.5). För att göra detta omvandlar vi kurvorna: ,
, .
. ,
,
 .
. .
. beskrivs av ekvationerna:
beskrivs av ekvationerna:
 motsvarande ansökningar
motsvarande ansökningar  punkter i området
punkter i området  variera inom.
variera inom. .
. bestäms av ojämlikheter
bestäms av ojämlikheter ,
,
 ,
, - envärdiga kontinuerliga funktioner på
- envärdiga kontinuerliga funktioner på  , Den där
, Den där
 ,
,
 ,
, ,
, (
( ,
, ,
, ).
). det finns en triangel
det finns en triangel  , avgränsad av raka linjer
, avgränsad av raka linjer  ,
, ,
, (Fig. 1.8). På
(Fig. 1.8). På  prickapplikationer
prickapplikationer  tillfredsställa ojämlikheten
tillfredsställa ojämlikheten  , Det är därför
, Det är därför .
.
 , vi får
, vi får


 ,
,
 ,,
,, ,
, ,
, .
. lika
lika  .
.
 , och ovanför planet
, och ovanför planet  (Fig. 1.10). Projektionsområde
(Fig. 1.10). Projektionsområde  det finns en cirkel
det finns en cirkel  med centrum vid origo och enhetsradie.
med centrum vid origo och enhetsradie. ,
, ,
, . På
. På  prickapplikationer
prickapplikationer  , tillfredsställa ojämlikheten
, tillfredsställa ojämlikheten
 ,
, .
. ,
, ,
,
 vi hittar med formeln (2.3):
vi hittar med formeln (2.3): .
. mellan axeln
mellan axeln  och normalt
och normalt  - dumt och därför
- dumt och därför  måste vara negativ. Med tanke på att
måste vara negativ. Med tanke på att  , på en yta
, på en yta  vi får
vi får
 .
. :
: , belägen i den första oktanten. Ekvationen för detta plan i segment har formen
, belägen i den första oktanten. Ekvationen för detta plan i segment har formen
 , enhet normal vektor
, enhet normal vektor
 .
. .
. ,
,
 , var
, var  , därav,
, därav, var
var