Преобразуване двоен интегралот правоъгълни координати, до полярни координати
, свързани с правоъгълни координати чрез отношенията
,
, се извършва по формулата

Ако домейнът на интеграция
ограничен до два лъча
,
(
), излизаща от полюса, и две криви
И
, тогава двойният интеграл се изчислява по формулата

Пример 1.3.Изчислете площта на фигурата, ограничена от тези линии:
,
,
,
.

Решение.За изчисляване на площта на площ
Нека използваме формулата:
.

Нека изобразим района
(фиг. 1.5). За да направим това, трансформираме кривите:

,
,

,
.

Да преминем към полярните координати:

,
.

В полярната координатна система областта
описани с уравненията:

1.2. Тройни интеграли

Основните свойства на тройните интеграли са подобни на свойствата на двойните интеграли.

IN Декартови координатиТройният интеграл обикновено се записва така:

Ако
, след това тройният интеграл върху областта числено равен на обема на тялото :

Изчисление на троен интеграл

Нека домейнът на интеграция ограничени отдолу и отгоре съответно от еднозначни непрекъснати повърхности
,
, и проекцията на региона към координатната равнина
има равна площ
(фиг. 1.6).

След това за фиксирани стойности
съответните приложения точки от областта варират в рамките на.

Тогава получаваме:

Ако освен това проекцията
определени от неравенства

,
,

Където
- недвусмислено непрекъснати функцииНа
, Че

Пример 1.4.Изчисли
, Където - тяло, ограничено от равнини:

,
,
,
(
,
,
).

Решение.Областта на интеграция е пирамида (фиг. 1.7). Прожекционна зона има триъгълник
, ограничени с прави линии
,
,
(фиг. 1.8). При
прилага се точка
удовлетворяват неравенството
, Ето защо

Задаване на границите на интегриране за триъгълник
, получаваме

Троен интеграл в цилиндрични координати

При движение от декартови координати
към цилиндрични координати
(фиг. 1.9), свързана с
отношения
,
,
, и

,
,,

тройният интеграл се трансформира:

Пример 1.5.Изчислете обема на тяло, ограничено от повърхности:
,
,
.

Решение.Необходим обем на тялото равно на
.

Областта на интегриране е част от цилиндър, ограничен отдолу с равнина
, и над самолета
(фиг. 1.10). Прожекционна зона има кръг
с център в началото и единичен радиус.

Да преминем към цилиндричните координати.
,
,
. При
прилага се точка
, удовлетворяват неравенството

или в цилиндрични координати:

Регион
, ограничена от крива
, ще приеме формата, или
, докато полярният ъгъл
. В резултат на това имаме

2. Елементи на теорията на полето

Нека първо си припомним методите за изчисляване на криволинейни и повърхностни интеграли.

Изчисляване на криволинеен интеграл по координати на функции, дефинирани върху крива , се свежда до изчисляване на определен интеграл на формата

ако кривата определени параметрично
съответства на началната точка на кривата , А
- крайната му точка.

Изчисляване на повърхностен интеграл на функция
, определени върху двустранна повърхност , се свежда до изчисляване на двоен интеграл, например, на формата

ако повърхността , дадено от уравнението
, се проектира уникално върху самолета
към региона
. Тук - ъгъл между единичен нормален вектор на повърхността и ос
:

Страната на повърхността, изисквана от проблемните условия се определя от избора на съответния знак във формула (2.3).

Определение 2.1. Векторно поле
наречена векторна функция на точка
заедно с неговия обхват:

Векторно поле
характеризира се със скаларна величина – разминаване:

Определение 2.2. Поток векторно поле
през повърхността наречен повърхностен интеграл:

Където - единичен нормален вектор към избраната страна на повърхността , А
- скаларно произведениевектори И .

Определение 2.3. Тираж векторно поле

от затворена крива наречен криволинеен интеграл

Където
.

Формула на Остроградски-Гаус установява връзка между нишка векторно поле през затворена повърхност и дивергенция на полето:

Където - повърхност, ограничена от затворен контур , А е единичният нормален вектор към тази повърхност. Посоката на нормалата трябва да съответства на посоката на преминаване на контура .

Пример 2.1.Изчисляване на повърхностен интеграл

Където - външна част на конуса
(
), отсечен от самолет
(Фигура 2.1).

Решение.Повърхност уникално проектирани в региона
самолет
, а интегралът се изчислява по формула (2.2).

Нормален вектор на единична повърхност намираме с помощта на формула (2.3):

Тук в израза за нормалата е избран знакът плюс, тъй като ъгълът между оста
и нормално - глупав и следователно
трябва да е отрицателен. Като се има предвид това
, върху повърхност получаваме

Регион
има кръг
. Следователно в последния интеграл преминаваме към полярни координати, докато
,
:

Пример 2.2.Намерете дивергенцията и извивката на векторно поле
.

Решение.Използвайки формула (2.4), получаваме

Роторът на дадено векторно поле се намира по формула (2.5)

Пример 2.3.Намерете потока на векторно поле
през част от самолета :
, разположен в първия октант (нормалата образува остър ъгъл с оста
).

Решение.По силата на формула (2.6)

Нека изобразим част от самолета :
, разположен в първи октант. Уравнението на тази равнина в сегменти има формата

(фиг. 2.3). Нормалният вектор към равнината има координати:
, единичен нормален вектор

,
, където
, следователно,

Където
- равнинна проекция На
(фиг. 2.4).

Пример 2.4.Изчислете потока на векторно поле през затворена повърхност , образувана от равнината
и част от конуса
(
) (фиг. 2.2).

Решение.Нека използваме формулата на Остроградски-Гаус (2.8)

Нека намерим дивергенцията на векторното поле по формула (2.4):

Където
е обемът на конуса, върху който се извършва интегриране. Нека използваме добре познатата формула за изчисляване на обема на конус
(- радиус на основата на конуса, - неговото високо). В нашия случай получаваме
. Накрая получаваме

Пример 2.5.Изчислете циркулацията на векторно поле
по контура , образувана от пресичането на повърхности
И
(
). Проверете резултата, като използвате формулата на Стокс.

Решение.Пресечната точка на тези повърхности е кръг
,
(фиг. 2.1). Посоката на преминаване обикновено се избира така, че ограничената от нея зона да остане отляво. Нека напишем параметричните уравнения на контура :

където

и параметъра варира от преди
. Използвайки формула (2.7), като вземем предвид (2.1) и (2.10), получаваме

Нека сега приложим формулата на Стокс (2.9). Като повърхност , опъната по контура , можете да вземете част от самолета
. Нормална посока
към тази повърхност е в съответствие с посоката на преминаване на контура . Извивката на дадено векторно поле се изчислява в Пример 2.2:
. Следователно желаният тираж

Където
- площ на района
.
- радиус на кръга
, където

Нека имаме две правоъгълни координатни системи в пространството и
и система от функции

(1)

които установяват едно-към-едно съответствие между точки в някои области
И
в тези координатни системи. Да приемем, че функциите на система (1) имат
непрекъснати частични производни. Детерминантата, съставена от тези частични производни

се нарича якобиан (или детерминант на Якоби) на системата от функции (1). Ще приемем, че
V
.

При направените по-горе допускания е валидна следната обща формула за промяна на променливи в троен интеграл:

Както в случая с двойния интеграл, взаимната уникалност на системата (1) и условието
могат да бъдат нарушени в отделни точки, на отделни линии и на отделни повърхности.

Система от функции (1) за всяка точка
съвпада с една точка
. Тези три числа
се наричат криволинейни координати на точка . Точки от пространството
, за които една от тези координати запазва постоянна стойност, образуват т.нар. координатна повърхност.

II Троен интеграл в цилиндрични координати

Цилиндричната координатна система (CSS) се определя от равнината
, в която е зададена полярна координатна система и ос
, перпендикулярна на тази равнина. Цилиндрични координати на точка
, Където
– полярни координатиточки – прогнози t очила до самолета
, А – това са координатите на проекцията на точката на ос
или
.

В самолета
въвеждаме декартови координати по обичайния начин, насочваме оста на приложението по оста
CSK. Сега не е трудно да се получат формули, свързващи цилиндрични координати с декартови:

(3)

Тези формули картографират площта към цялото пространство
.

Координатните повърхности в разглеждания случай ще бъдат:

1)
– цилиндрични повърхнини с образуващи, успоредни на оста
, чиито водачи са кръгове в равнината
, центрирана в точка ;

2)

;

3)
– равнини, успоредни на равнината
.

Якобиан на система (3):

Общата формула в случая на CSK приема формата:

Бележка 1 . Преходът към цилиндрични координати се препоръчва в случаите, когато зоната на интегриране е кръгов цилиндър или конус, или параболоид на въртене (или части от него), а оста на това тяло съвпада с оста на приложението
.

Бележка 2. Цилиндричните координати могат да бъдат обобщени по същия начин като полярните координати в равнина.

Пример 1. Изчислете тройния интеграл на функция

по региони
, представляваща вътрешната част на цилиндъра
, ограничена от конус
и параболоид
.

Решение. Вече разгледахме тази област в §2, пример 6 и получихме стандартен запис в DPSC. Изчисляването на интеграла в тази област обаче е трудно. Да отидем на CSK:

Проекция
тяло
до самолета
- това е кръг
. Следователно координатата варира от 0 до
, А – от 0 до Р. През произволна точка
начертайте права линия, успоредна на оста
. Правата линия ще влезе в
на конус, но ще излезе на параболоид. Но конусът
има уравнението в CSC
, и параболоида
- уравнението
. Така че имаме

III Троен интеграл в сферични координати

Сферичната координатна система (СКС) се определя от равнината
, в който е посочен UCS, и ос
, перпендикулярна на равнината
.

Сферични координати на точка пространството се нарича тройка числа
, Където – полярен ъгъл на проекция на точка върху равнина
,– ъгъл между осите
и вектор
И
.

В самолета
нека въведем декартови координатни оси
И
по обичайния начин и оста на приложението е съвместима с оста
. Формулите, свързващи сферичните координати с декартовите са следните:

(4)

Тези формули картографират площта към цялото пространство
.

Якобиан на системата от функции (4):

Има три семейства координатни повърхности:

1)
– концентрични сфери с център в началото;

2)
– полуравнини, минаващи през оста
;

3)
– кръгови конуси с връх в началото на координатите, чиято ос е ос
.

Формула за преход към SSC в троен интеграл:

Бележка 3. Преходът към SCS се препоръчва, когато домейнът на интеграция е топка или част от нея. В този случай уравнението на сферата
отива в. Подобно на CSK, обсъден по-рано, CSK е „вързан“ към оста
. Ако центърът на сферата се измести с радиус по координатната ос, тогава получаваме най-простото сферично уравнение, когато се измести по оста
:

Бележка 4. Възможно е да се обобщи SSC:

с Якобиан
. Тази система от функции ще транслира елипсоида

към "паралелепипед"

Пример 2. Намерете средното разстояние на точките върху топка с радиус от центъра му.

Решение. Спомнете си, че средната стойност на функцията
в района
е тройният интеграл на функция върху регион, разделен на обема на региона. В нашия случай

Така че имаме

Тройни интеграли. Изчисляване на обема на тялото.
Троен интеграл в цилиндрични координати

Три дни мъртвецът лежи в кабинета на декана, облечен в панталоните на Питагор,
В ръцете на Фихтенхолц той държеше том, който го бе довел от този свят,
За краката беше вързан троен интеграл, а трупът беше увит в матрица,
И вместо да се моли, някакъв нагъл човек прочете теоремата на Бернули.

Тройните интеграли са нещо, от което не трябва да се страхувате =) Защото, ако четете този текст, тогава най-вероятно имате добро разбиране теория и практика на “обикновените” интеграли, и двойни интеграли. И където има двойно, наблизо има тройка:

И наистина, какво има да се страхувам? Интегралът е по-малък, интегралът е повече....

Да погледнем записа:

– тройна интегрална икона;
– интегрант функция на три променливи;
– произведение на диференциали.
– зона на интеграция.

Нека се съсредоточим специално върху области на интеграция. Ако в двоен интегралпредставлява плоска фигура, тогава тук – пространствено тяло, която, както е известно, е ограничена от множеството повърхности. По този начин, в допълнение към горното, трябва да навигирате основни повърхности на пространствотои да могат да правят прости триизмерни рисунки.

Някои са депресирани, разбирам... Уви, статията не може да бъде озаглавена „тройни интеграли за манекени“, а има някои неща, които трябва да знаете/умеете да правите. Но няма страшно - целият материал е представен в изключително достъпна форма и може да бъде усвоен за възможно най-кратко време!

Какво означава да се изчисли троен интеграл и какво е четен?

Да се изчисли средната стойност на тройния интеграл намери ЧИСЛОТО:

В най-простия случай, когато тройният интеграл е числено равен на обема на тялото. И наистина, според общо значение на интеграцията, произведението е равно безкрайно малъкобемът на елементарна „тухла“ от тялото. И тройният интеграл е справедлив обединява всички тези безкрайно малки частицивърху площта, което води до интегралната (общата) стойност на обема на тялото: .

Освен това тройният интеграл има важно значение физически приложения. Но повече за това по-късно - във 2-ра част на урока, посветена на изчисления на произволни тройни интеграли, които имат функция в общ случайе различно от постоянно и непрекъснато в региона. В тази статия ще разгледаме подробно проблема с намирането на обем, който според моята субективна оценка се среща 6-7 пъти по-често.

Как се решава троен интеграл?

Отговорът логично следва от предходния параграф. Трябва да се определи ред на преминаване на тялотои отидете на итерирани интеграли. След това се занимавайте последователно с три единични интеграла.

Както можете да видите, цялата кухня много, много напомня двойни интеграли, с тази разлика, че сега сме добавили допълнително измерение (грубо казано височина). И вероятно много от вас вече са се досетили как се решават тройните интеграли.

Нека разсеем всички останали съмнения:

Пример 1

Моля, запишете в колона на хартия:

И отговорете на следните въпроси. Знаете ли кои повърхности определят тези уравнения? Разбирате ли неформалното значение на тези уравнения? Можете ли да си представите как са разположени тези повърхности в пространството?

Ако сте склонни към общия отговор „по-скоро не, отколкото да“, тогава не забравяйте да работите през урока, в противен случай няма да напреднете повече!

Решение: използваме формулата.

За да разберете ред на преминаване на тялотои отидете на итерирани интегралитрябва (всичко гениално е просто) да разберете какъв вид тяло е това. И в много случаи рисунките значително допринасят за такова разбиране.

По условие тялото е ограничено от няколко повърхности. Откъде да започнем да строим? Предлагам следната процедура:

Първо нека изобразим паралелен ортогоналенпроекция на тялото върху координатната равнина. За първи път казах как се нарича тази проекция, хаха =)

Тъй като проекцията се извършва по оста, тогава на първо място е препоръчително да се справите с повърхности, които са успоредни на тази ос. Нека ви напомня, че уравненията на такива повърхности не съдържат буквата "z". В разглеждания проблем има три от тях:

– уравнението задава координатна равнина, която минава през оста;
– уравнението задава координатна равнина, която минава през оста;
– наборите от уравнения самолет "плоска" права линияуспоредна на оста.

Най-вероятно желаната проекция е следният триъгълник:

Може би не всички са разбрали напълно за какво говорим. Представете си, че една ос излиза от екрана на монитора и се забива директно в моста на носа ви ( тези. оказва се, че гледате триизмерна рисунка отгоре). Изследваното пространствено тяло е разположено в безкраен тристенен „коридор“ и проекцията му върху равнина най-вероятно представлява защрихован триъгълник.

Бих искал да обърна специално внимание на факта, че докато сме изразили просто предположение за проекцияи клаузите „най-вероятно” и „най-вероятно” не са случайни. Факт е, че не всички повърхности все още са анализирани и може да се случи някоя от тях да „отсече“ част от триъгълника. Като ясен пример това предполага сферас център в началото на радиус по-малък от едно, например сфера – неговата проекция върху равнината (окръжност ) няма да „покрие“ напълно защрихованата зона и крайната проекция на тялото изобщо няма да бъде триъгълник (кръгът ще "отреже" острите си ъгли).

На втория етап откриваме как тялото е ограничено отгоре и отдолу и извършваме пространствена рисунка. Нека се върнем към постановката на проблема и да видим кои повърхности остават. Уравнението определя самата координатна равнина, а уравнението – параболичен цилиндър, разположен по-гореравнина и минаваща през оста. Така проекцията на тялото е наистина триъгълник.

Между другото, намерих го тук съкращаванеусловия - не е необходимо да се включва уравнението на равнината, тъй като повърхността, докосваща абсцисната ос, вече затваря тялото. Интересно е да се отбележи, че в този случай няма да можем веднага да начертаем проекцията - триъгълникът ще "начертае" само след анализ на уравнението.

Нека внимателно изобразим фрагмент от параболичен цилиндър:

След завършване на чертежите с редът на ходене около тялотоняма проблем!

Първо, определяме реда на обхождане на проекцията (в същото време е МНОГО ПО-УДОБНО да навигирате с помощта на двуизмерен чертеж).Готово е ТОЧНО СЪЩОТО, Както в двойни интеграли! Помислете за лазерна показалка и сканиране на плоска област. Нека изберем „традиционния“ 1-ви байпасен метод:

След това вземаме магически фенер, разглеждаме триизмерната рисунка и строго отдолу нагореОсветяваме пациента. Лъчите влизат в тялото през равнина и излизат през повърхността. Така редът на преминаване на тялото е:

Нека да преминем към повтарящи се интеграли:

1) Трябва да започнете с "зета" интеграла. Ние използваме Формула на Нютон-Лайбниц:

Нека заместим резултата в интеграла на „играта“:

Какво стана? По същество решението беше сведено до двоен интеграл и точно до формулата обем на цилиндрична греда! Следното е познато:

Обърнете внимание на рационалната техника за решаване на 3-ти интеграл.

Отговор:

Изчисленията винаги могат да бъдат записани в „един ред“:

Но бъдете внимателни с този метод - увеличаването на скоростта е изпълнено със загуба на качество и колкото по-сложен е примерът, толкова по-голям е шансът да направите грешка.

Да отговорим на един важен въпрос:

Необходимо ли е да се правят чертежи, ако условията на задачата не изискват тяхното изпълнение?

Можете да отидете по четири начина:

1) Начертайте проекцията и самото тяло. Това е най-изгодният вариант - ако имате възможност да завършите две прилични рисунки, не бъдете мързеливи, направете и двете рисунки. Първо го препоръчвам.

2) Начертайте само тялото. Подходящо, когато тялото има проста и очевидна проекция. Така например в разглобения пример би бил достатъчен триизмерен чертеж. Има обаче и минус - неудобно е да се определи редът на преминаване на проекцията от 3D картина и бих препоръчал този метод само на хора с добро ниво на подготовка.

3) Начертайте само проекцията. Това също не е лошо, но тогава се изискват допълнителни писмени коментари, което ограничава областта от различни страни. За съжаление, третият вариант често е принуден - когато тялото е твърде голямо или конструкцията му е изпълнена с други трудности. И ние също ще разгледаме такива примери.

4) Изобщо без чертежи. В този случай трябва да си представите тялото мислено и да коментирате писмено неговата форма/местоположение. Подходящ за много прости тела или задачи, при които изпълнението на двете чертежи е трудно. Но все пак е по-добре да направите поне схематичен чертеж, тъй като „голото“ решение може да бъде отхвърлено.

Следният орган е за самостоятелна работа:

Пример 2

С помощта на троен интеграл изчислете обема на тяло, ограничено от повърхности

В този случай областта на интегриране се определя предимно от неравенства, а това е още по-добре - набор от неравенства определя 1-ви октант, включително координатни равнини, и неравенството – полупространство, съдържащ произхода (проверете)+ самият самолет. „Вертикалната“ равнина пресича параболоида по параболата и е препоръчително да се изгради този участък в чертежа. За да направите това, трябва да намерите допълнителна референтна точка, най-лесният начин е върхът на параболата (разглеждаме стойностите и изчислете съответния „zet“).

Нека продължим да загряваме:

Пример 3

С помощта на троен интеграл изчислете обема на тялото, ограничено от посочените повърхнини. Изпълнете чертежа.

Решение: Формулировката „изпълнете чертеж“ ни дава известна свобода, но най-вероятно предполага изпълнението на пространствен чертеж. Проекцията обаче също няма да навреди, особено след като тук не е най-простата.

Придържаме се към вече доказаните тактики - първо ще се справим повърхности, които са успоредни на оста на приложението. Уравненията на такива повърхности не съдържат изрично променливата "z":

– уравнението определя координатната равнина, минаваща през оста ( което на равнината се определя от „едноименното“ уравнение);
– наборите от уравнения самолет, преминавайки през „едноименния“ "плоска" права линияуспоредна на оста.

Желаното тяло е ограничено от равнина отдолу и параболичен цилиндъргоре:

Нека създадем ред на преминаване на тялото, докато границите на интеграция „X“ и „Y“, напомням ви, е по-удобно да разберете с помощта на двуизмерен чертеж:

По този начин:

Когато интегрирате върху „y“, „x“ се счита за константа, така че е препоръчително незабавно да извадите константата от интегралния знак.

Отговор:

Да, почти забравих, в повечето случаи е малко полезно (и дори вредно) да проверявате получения резултат с триизмерна рисунка, тъй като с голяма вероятност илюзия за обем, за което говорих в клас Обем на въртеливото тяло. Така че, оценявайки тялото на разглеждания проблем, лично на мен ми се стори, че има много повече от 4 „кубчета“.

Следният пример за независимо решение:

Пример 4

С помощта на троен интеграл изчислете обема на тялото, ограничено от посочените повърхнини. Направете рисунки на това тяло и неговата проекция върху равнина.

Примерен пример за задача в края на урока.

Не е необичайно, когато изпълнението на триизмерна рисунка е трудно:

Пример 5

Използвайки троен интеграл, намерете обема на тяло, даден от неговите гранични повърхности

Решение: проекцията тук не е сложна, но трябва да помислите за реда на преминаването й. Ако изберете първия метод, тогава фигурата ще трябва да бъде разделена на 2 части, което сериозно заплашва да изчисли сумата дветройни интеграли. В това отношение вторият път изглежда много по-обещаващ. Нека изразим и изобразим проекцията на това тяло на чертежа:

Извинявам се за качеството на някои от снимките, изрязах ги директно от собствените си ръкописи.

Избираме по-изгоден ред на преминаване на фигурата:

Сега всичко зависи от тялото. Отдолу тя е ограничена от равнината, отгоре - от равнината, която минава през ординатната ос. И всичко би било наред, но последната равнина е твърде стръмна и изграждането на района не е толкова лесно. Изборът тук е незавиден: или бижутерска работа в малък мащаб (тъй като тялото е доста тънко), или рисунка с височина около 20 сантиметра (и дори тогава, ако пасне).

Но има и трети, роден руски метод за решаване на проблема - да вкарате =) И вместо триизмерна рисунка, задоволете се с устно описание: „Това тяло е ограничено от цилиндри и равнина отстрани, равнина отдолу и равнина отгоре.”

„Вертикалните“ граници на интеграцията очевидно са:

Нека изчислим обема на тялото, като не забравяме, че заобиколихме проекцията по по-рядко срещан начин:

Отговор:

Както забелязахте, телата, предложени в задачи, които не са по-скъпи от сто долара, често са ограничени от равнината по-долу. Но това не е правило, така че винаги трябва да сте нащрек - може да попаднете на задача, където се намира тялото и подапартамент Така например, ако в анализирания проблем вместо това разгледаме равнината, тогава изследваното тяло ще бъде симетрично картографирано в долното полупространство и ще бъде ограничено от равнината отдолу и от равнината отгоре!

Лесно се вижда, че получавате същия резултат:

(не забравяйте, че тялото трябва да се разхожда строго отдолу нагоре!)

Освен това „любимият“ самолет може изобщо да не се използва, най-прост пример: топка, разположена над равнината - при изчисляване на нейния обем изобщо няма да е необходимо уравнение.

Ще разгледаме всички тези случаи, но засега има подобна задача, която да решите сами:

Пример 6

Използвайки тройния интеграл, намерете обема на тяло, ограничено от повърхности

Кратко решение и отговор в края на урока.

Нека да преминем към втория параграф с еднакво популярни материали:

Троен интеграл в цилиндрични координати

Цилиндричните координати по същество са полярни координатив космоса.
В цилиндрична координатна система позицията на точка в пространството се определя от полярните координати на точката - проекцията на точката върху равнината и приложението на самата точка.

Преход от триизмерно Декартова системакъм цилиндричната координатна система се извършва по следните формули:

Във връзка с нашата тема, трансформацията изглежда така:

И съответно в опростения случай, който разглеждаме в тази статия:

Основното нещо е да не забравяте за допълнителния множител "er" и да го поставите правилно полярни граници на интеграцияпри преминаване на проекцията:

Пример 7

Решение: ние се придържаме към същата процедура: първо, разглеждаме уравнения, в които променливата „ze“ отсъства. Тук има само един. Проекция цилиндрична повърхноствърху самолета представлява „едноименния“ кръг .

Самолети те ограничават желаното тяло отдолу и отгоре („изрязват“ го от цилиндъра) и го проектират в кръг:

Следва триизмерна рисунка. Основната трудност се състои в конструирането на равнина, която пресича цилиндъра под "наклонен" ъгъл, което води до елипса. Нека изясним този раздел аналитично: за да направим това, пренаписваме уравнението на равнината във функционална форма и изчислете стойностите на функцията („височина“) в очевидните точки, които лежат на границата на проекцията:

Маркираме намерените точки върху чертежа и внимателно (не като мен =))свържете ги с линия:

Проекцията на тяло върху равнина е кръг и това е силен аргумент в полза на преминаването към цилиндрична координатна система:

Нека намерим уравненията на повърхности в цилиндрични координати:

Сега трябва да разберете реда на преминаване на тялото.

Първо, нека се заемем с проекцията. Как да определим реда на неговото преминаване? ТОЧНО СЪЩИЯТ КАТО С изчисляване на двойни интеграли в полярни координати. Тук е елементарно:

„Вертикалните“ граници на интеграция също са очевидни - ние влизаме в тялото през равнината и излизаме от него през равнината:

Нека да преминем към повтарящи се интеграли:

В този случай ние незабавно поставяме фактора „er“ в „нашия“ интеграл.

Както обикновено, метлата е по-лесна за чупене по клонките:

Поставяме резултата в следния интеграл:

И тук не забравяме, че "фи" се счита за константа. Но това е за момента:

Отговор:

Подобна задача, която можете да решите сами:

Пример 8

Изчислете обема на тяло, ограничено от повърхности, като използвате троен интеграл. Начертайте чертежи на това тяло и неговата проекция върху равнина.

Приблизителна проба на окончателния дизайн в края на урока.

Моля, имайте предвид, че в условията на задачите не се казва нито дума за прехода към цилиндрична координатна система и невеж човек ще се бори с трудни интеграли в декартови координати. ...Или може би няма - все пак има трети, оригинален руски начин за решаване на проблеми =)

Едва започва! ...в добрия смисъл: =)

Пример 9

Използвайки тройния интеграл, намерете обема на тяло, ограничено от повърхности

Скромно и с вкус.

Решение: това тяло е ограничено конична повърхностИ елипсовиден параболоид. Читатели, които са прочели внимателно материалите на статията Основни повърхности на пространството, вече са си представили как изглежда тялото, но на практика често има по-сложни случаи, така че ще направя подробно аналитично разсъждение.

Първо намираме линиите, по които се пресичат повърхностите. Нека съставим и решим следната система:

От първото уравнение изваждаме втория член по член:

Резултатът е два корена:

Нека заместим намерената стойност във всяко уравнение на системата:
, от което следва, че
Така коренът съответства на една единствена точка - началото. Естествено, защото върховете на разглежданите повърхности съвпадат.

Сега нека заместим втория корен – също във всяко уравнение на системата:

Какъв е геометричният смисъл на получения резултат? „На височина“ (в равнината) параболоидът и конусът се пресичат кръг– единичен радиус с център в точка .

Следователно в този случай "купата" на параболоида съдържа "фунията" на конуса формиранеКоничната повърхност трябва да бъде начертана с пунктирана линия (с изключение на най-отдалечения от нас сегмент на генератора, който се вижда от този ъгъл):

Проекцията на тяло върху равнина е кръгс център в началото на радиус 1, който дори не си направих труда да изобразя поради очевидността на този факт (ние обаче предоставяме писмен коментар!). Между другото, в предишните две задачи чертежът на проекцията също може да бъде оценен, ако не беше условието.

При преминаване към цилиндрични координати с помощта на стандартни формули неравенството се записва в най-простата му форма и няма проблеми с реда на преминаване на проекцията:

Нека намерим уравненията на повърхности в цилиндрична координатна система:

Тъй като задачата разглежда горната част на конуса, изразяваме от уравнението:

„Ние сканираме тялото“ отдолу нагоре. През него влизат светлинни лъчи елипсовиден параболоиди излизат през коничната повърхност. По този начин "вертикалният" ред на преминаване на тялото е:

Останалото е въпрос на техника:

Отговор:

Не е необичайно едно тяло да се определя не от неговите гранични повърхности, а от много неравенства:

Пример 10

Геометрично значениеОбясних пространствените неравенства достатъчно подробно в същата референтна статия - Основни повърхности на пространството и тяхното изграждане.

Тази задачавъпреки че съдържа параметър, той позволява изпълнението на точен чертеж, който отразява основния вид на тялото. Помислете как да изградите. Кратко решение и отговор има в края на урока.

...е, още няколко задачи? Мислех си да довърша урока, но просто чувствам, че искаш още =)

Пример 11

С помощта на троен интеграл изчислете обема на дадено тяло:
, където е произволно положително число.

Решение: неравенство дефинира топка с център в началото на радиуса и неравенството – „вътрешността“ на кръгъл цилиндър с ос на симетрия на радиус . Така желаното тяло е ограничено от кръгъл цилиндър отстрани и сферични сегменти, симетрични спрямо равнината отгоре и отдолу.

Като вземем това за основна мерна единица, нека начертаем:

По-точно трябва да се нарече рисунка, тъй като не поддържах добре пропорциите по оста. Честно казано обаче условието не изискваше да се рисува абсолютно нищо и подобна илюстрация се оказа напълно достатъчна.

Моля, обърнете внимание, че тук не е необходимо да установявате височината, на която цилиндърът изрязва „шапките“ от топката - ако вземете компас в ръцете си и го използвате, за да маркирате кръг с център в началото на радиуса 2 см, тогава точките на пресичане с цилиндъра ще се появят сами.

Тройният интеграл се записва по следния начин:

Изчислете троен интеграл - означава намиране на число, равно на обема на тялото Vили, което е същото - области V .

Почти всеки може да разбере значението на изчисляването на троен интеграл "по трудния начин". По-точно - "под кожата", и още по-точно - в дихателните му органи - белите дробове. Независимо дали го знаете или не, в човешките бели дробове има над 700 милиона алвеоли - везикуларни образувания, преплетени с мрежа от капиляри. Обменът на газ се осъществява през стените на алвеолите. Следователно можем да разсъждаваме така: обемът газ в белите дробове може да бъде представен като някаква компактна област. И този обем се състои от малки обеми, концентрирани в алвеолите. Ключовата роля в това сравнение играе огромният брой алвеоли в белите дробове: както ще видим в следващия абзац, чрез такъв „огромен брой малки неща“ концепцията за троен интеграл е математически формулирана.

Защо тройният интеграл се използва за намиране на обема на тяло? V? Нека района Vразделена на нпроизволни области Δ vаз, като това обозначение означава не само всяка малка площ, но и нейния обем. Във всяка такава малка област се избира произволна точка Маз, А f(Ми)- стойност на функцията f(М) в този момент. Сега ще увеличим максимално броя на такива малки области и най-големия диаметър Δ vаз- напротив, намалете. Можем да съставим интегрална сума на формата

Ако функцията f(М) = f(х, г, z) е непрекъснато, то ще съществува граница на интегралната сума посочения по-горе тип. Тази граница се нарича троен интеграл .

В този случай функцията f(М) = f(х, г, z) наречен интегрируем на домейн V ; V- област на интеграция; х, г, z- интеграционни променливи, дв(или dx dy дз ) - елемент на обема.

Изчисляване на тройния интеграл чрез намаляване на кратността

Както в случая с двойните интеграли, изчисляването на тройните интеграли се свежда до изчисляването на интеграли с по-малка кратност.

Помислете за триизмерна област V. Отдолу и отгоре (т.е. във височина) тази зона е ограничена от повърхности z = z1 (х, г) И z = z2 (х, г) . Отстрани (т.е. по ширина) площта е ограничена от повърхности г = г1 (х) И г = г2 (х) . И накрая, в дълбочина (ако гледате областта по посока на оста вол) - повърхности х = аИ х = b

За да се приложи преходът към интеграли с по-малка кратност, се изисква триизмерната област Vбеше правилно. Правилно е, когато е прав, успоредна на оста Оз, пресича границата на региона Vна не повече от две точки. Правилните триизмерни области са например кубоид, елипсоид и тетраедър. Фигурата по-долу показва правоъгълен паралелепипед, който ще срещнем в първия пример за решаване на задача.

За да визуализираме разликата между правилността и неправилността, добавяме, че повърхностите на региона по височината на правилния регион не трябва да са вдлъбнати навътре. Фигурата по-долу е пример за неправилна област V- еднолистов хиперболоид, чиято повърхност е права, успоредна на оста Оз(червен), пресича се в повече от две точки.

Ще разгледаме само правилните области.

Така че областта V- правилно. Тогава за всяка функция f(х, г, z) , непрекъснато в обл V, формулата е валидна

Тази формула ви позволява да намалите изчисляването на тройния интеграл до последователното изчисляване на вътрешния определен интеграл върху променливата z(при постоянно хИ г) и външния двоен интеграл върху двумерна област д .

Преминавайки от двойния интеграл към повторения, получаваме следната формула за изчисляване на тройния интеграл:

По този начин, за да изчислите троен интеграл, трябва последователно да оцените три определени интеграла.

Тези интеграли се изчисляват от най-вътрешния (над променливата z) към най-външния (по променлива х). За да се направи последователността от изчисления по-лесна за разбиране, три „вложени“ интеграла могат да бъдат записани, както следва:

От този запис вече става ясно, че:

първо трябва да интегрирате функцията f(х, г, z) по променлива zи вземете уравненията като граници на интегриране z = z1 (х, г) И z = z2 (х, г) повърхности, ограничаващи района Vотдолу и отгоре;
г г = г1 (х) И г = г2 (х) повърхности, ограничаващи района Vот страни;
интегрирайте резултата, получен на предишната стъпка върху променливата хи вземете уравненията като граници на интегриране х = аИ х = bповърхности, ограничаващи района Vв дълбочина.

Пример 1.Нека преминем от троен интеграл към повторен интеграл

последователност от три определени интеграли. Оценете този повторен интеграл.

Решение. Изчисляването на итерирания интеграл винаги започва от последния интеграл:

Нека изчислим втория интеграл - по променливата г:

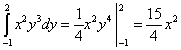х:

Отговор: Този повтарящ се интеграл и съответният му троен интеграл са равни на 10.

Пример 2.Изчислете троен интеграл

Където V- паралелепипед, ограничен от равнини х = − 1 , х = + 1 , г = 0 , г = 1 , z = 0 , z = 2 .

Решение. Границите на интегриране и за трите определени интеграла са еднозначно определени от уравненията на повърхнините, ограничаващи паралелепипеда. Следователно, ние незабавно редуцираме този троен интеграл до последователност от три определени интеграла:

Изчисляваме интеграла „в средата“ - над променливата г. Получаваме;

Сега изчисляваме най-външния интеграл - върху променливата х:

Отговор: Този троен интеграл е -2.

Пример 3.Изчислете троен интеграл

Където Vх + г + z = 1 и координатни равнини х = 0 , г = 0 , z= 0 . Регион Vпроектиран върху равнина xOyв триъгълник д, както е показано на фигурата по-долу.

Решение. Нека първо да определим границите на интеграцията. За интеграл върху променлива zдолната граница на интегриране е уникално определена: z= 0 . За да получим горната граница, ние изразяваме zот х + г + z = 1 . Получаваме 1 − х − г. За интеграл върху променлива гдолната граница на интегриране е уникално определена: г= 0 . За да получим горната граница, ние изразяваме гот х + г + z = 1 , като се има предвид това z= 0 (тъй като правата се намира в равнината xOy). Получаваме: 1 − х .

Редуцираме този троен интеграл до последователност от три определени интеграла:

Изчисляваме най-вътрешния интеграл - върху променлива z, като се вземат предвид константите x и y. Получаваме:

г. Получаваме:

х:

Отговор: Този троен интеграл е равен на 1/8.

Изчислете сами тройния интеграл и след това вижте решението

Пример 4.Изчислете троен интеграл

Където V- пирамида, ограничена от равнина х + г + z = 1 и координатни равнини х = 0 , г = 0 , z = 0 .

Подреждане на границите на интегриране при преминаване към редица от три интеграла

Случва се студенти, които нямат особени затруднения при директното изчисляване на интеграли, да не могат да свикнат да задават границите на интегриране, когато преминават от троен интеграл към последователност от три определени интеграла. Този въпрос изисква известно обучение. В първия пример, домейнът на интеграцията Vбеше паралелепипед, с който всичко е ясно: той е ограничен от всички страни с равнини, което означава, че границите на интегриране са еднозначно определени от уравненията на равнините. Във втория пример - пирамида: тук вече беше необходимо да помислим малко повече и да изразим една от границите от уравнението. И ако областта Vограничени ли са от неравни повърхности? Разбира се, необходимо е да се огледа района по определен начин V .

Да започнем с "по-страшен" пример, за да усетим "ситуацията, близка до бойна".

Пример 5.Подредете границите на интегриране при преминаване от троен интеграл, в който обл V- елипсоид

Решение. Нека центърът на елипсоида е началото, както е показано на фигурата по-горе. Нека погледнем елипсоида отдолу. Тя е ограничена отдолу от повърхност, която е тази част от повърхността на елипсоида, която се намира под равнината xOy zи полученият израз със знак минус ще бъде долната граница на интегриране върху променливата z:

Сега нека погледнем елипсоида отгоре. Тук тя е ограничена от повърхност, която е онази част от повърхността на елипсоида, която се намира над оста xOy. Следователно трябва да изразим от уравнението на елипсоида zи полученият израз ще бъде горната граница на интегриране върху променливата z:

Проекция на елипсоид върху равнина xOyе елипсоид. Неговото уравнение:

За получаване на долната граница на интегриране върху променлива г, трябва да бъдат изразени гот уравнението на елипсоида и вземете получения израз със знак минус:

За горната граница на интегриране върху променлива гсъщият израз със знак плюс:

Относно интегрирането върху променлива х, след това областта Vограничени в дълбочина от равнини. Следователно, границите на интегриране върху променлива хмогат да бъдат представени като координати на задната и предната граница на района. В случай на елипсоид, те ще бъдат стойностите на дължините на полуосите, взети с отрицателни и положителни знаци а: х1 = − а И х2 = а .

Така последователността от интеграли за изчисляване на обема на елипсоид е следната:

където „yrek first“, „yrek second“, „zet first“ и „zet second“ са изразите, получени по-горе. Ако имате желанието и смелостта да изчислите този интеграл и следователно обема на елипсоида, тогава ето отговора: 4 πabc/3 .

Следните примери не са толкова страшни, колкото току-що обсъдения. Освен това те включват не само определяне на границите на интегриране, но и изчисляване на самия троен интеграл. Тествайте какво сте научили, като следвате решението на страшния пример. Все още трябва да мислите, когато поставяте ограничения.

Пример 6.Изчислете троен интеграл

ако интеграционният домейн е ограничен от равнини х + г = 1 , х + 2г = 4 , г = 0 , г = 1 , z = 1 , z = 5 .

Решение. Примерът „курорт“ се сравнява с пример 5, тъй като границите на интеграция над „Y“ и „Z“ са уникално дефинирани. Но ще трябва да се справим с границите на интеграция над "X". Проекция на областта на интегриране върху равнината xOyе трапец ABCD.

В този пример е по-изгодно трапецът да се проектира върху оста Ой, в противен случай, за да изчислите тройния интеграл, ще трябва да разделите фигурата на три части. В Пример 4 започнахме да изследваме интеграционния регион отдолу и това е обичайната процедура. Но в този пример започваме проверката отстрани или, ако е по-лесно, поставяме фигурата отстрани и считаме, че я гледаме отдолу. Можем да намерим границите на интегриране върху "X" чисто алгебрично. За да направим това, ние изразяваме „x“ от първото и второто уравнения, дадени в примерното условие. От първото уравнение получаваме долната граница 1 − г, от втория - горен 4 − 2 г. Нека намалим този троен интеграл до последователност от три определени интеграла:

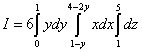внимание! В този пример най-външният интеграл не е върху променливата „x“, а върху променливата „y“, а „средният“ интеграл е върху променливата „x“! Тук приложихме промяна в реда на интегриране, с който се запознахме при изучаването на двойния интеграл. Това се дължи на факта, че, както вече беше споменато, ние започнахме да изследваме интеграционния регион не отдолу, а отстрани, тоест ние го проектирахме не върху оста вол, на ос Ой.

Изчисляваме най-вътрешния интеграл - върху променлива z, като се вземат предвид константите x и y. Получаваме:

Изчисляваме средния интеграл - върху променлива х. Получаваме:

Накрая изчисляваме най-външния интеграл - върху променливата г:

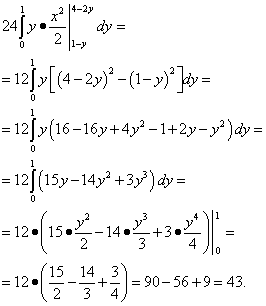
Отговор: Този троен интеграл е равен на 43.

Пример 7.Изчислете троен интеграл

ако областта на интегриране е ограничена до повърхности х = 0 , г = 0 , z = 2 , х + г + z = 4 .

Решение. Регион V(пирамида MNRP) е вярно. Прожекционна зона Vдо самолета xOyе триъгълник AOB.

Долните граници на интегриране за всички променливи са посочени в примерното условие. Нека намерим горната граница на интегриране върху "X". За да направим това, изразяваме "x" от четвъртото уравнение, като броим "y" равно на нула, а "зет" е равно на две. Получаваме х= 2. Нека намерим горната граница на интеграция над "играта". За да направим това, нека изразим "Y" от същото четвърто уравнение, като считаме, че "Z" е равно на две, а "X" е променлива стойност. Получаваме г = 2 − х. И накрая, намираме горната граница на интегриране върху променливата "z". За да направим това, изразяваме „zet“ от същото четвърто уравнение, като броим „y“ и „zet“ променливи количества. Получаваме z = 4 − х − г .

Нека намалим този троен интеграл до последователност от три определени интеграла:

Изчисляваме най-вътрешния интеграл - върху променлива z, като се вземат предвид константите x и y. Получаваме:

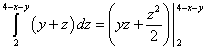Изчисляваме средния интеграл - върху променлива г. Получаваме:

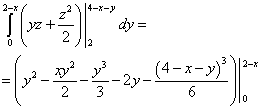Изчисляваме най-външния интеграл - върху променлива хи накрая намираме този троен интеграл:

Отговор: Този троен интеграл е равен на 2.

Промяна на променливи в троен интеграл и цилиндрични координати

Ако проекцията на интеграционния домейн върху която и да е от координатните равнини е кръг или част от кръг, тогава тройният интеграл е по-лесен за изчисляване чрез преминаване към цилиндрични координати. Цилиндричната координатна система е обобщение полярна координатна системакъм космоса. В цилиндрична координатна система, точка Мсе характеризира с три величини ( r, φ , z), Където r- разстояние от началото до проекцията нточки Мдо самолета xOy, φ - ъгъл между вектор НАи положителна посока на оста вол, z- точка на приложение М(снимката по-долу).

Правоъгълни координати х, г, zс цилиндрични координати r, φ , zсвържете формули

х = r cos φ ,

г = rгрях φ ,

z = z .

За да преминете към цилиндрични координати в троен интеграл, трябва да изразите интегралната функция като функция от променливи r, φ , z:

Тоест преходът от правоъгълни към цилиндрични координати се извършва, както следва:

Тройният интеграл в цилиндрични координати се изчислява по същия начин както в декартови правоъгълни координати, като се трансформира в последователност от три определени интеграла:

Пример 8.Изчислете троен интеграл

преход към цилиндрични координати, където V- площ, ограничена от повърхности и.

Решение. Тъй като областта Vдо самолета xOyсе проектира в кръг, след това координатата φ варира от 0 до 2 π , и координатата r- от r=0 до r=1. Постоянна стойност в пространството съответства на цилиндър. Като се има предвид пресечната точка на този цилиндър с региона V, получаваме промяна в ординатата zот z = rдо z= 1. Нека да преминем към цилиндричните координати и да получим.

1. Цилиндричните координати представляват връзката на полярните координати в равнината xy с обичайното декартово приложение z (фиг. 3).

Нека M(x, y, z) е произволна точка в пространството xyz, P е проекцията на точка M върху равнината xy. Точка M се определя еднозначно от тройка числа - полярни координати на точка P, z - приложение на точка M. Формулите, които ги свързват с декартовите, имат вида

Якобианско картографиране (8)

Пример 2.

Изчислете интеграл

където T е площта, ограничена от повърхности

Решение. Нека преместим интеграла в сферични координати с помощта на формули (9). Тогава областта на интегриране може да бъде определена от неравенствата

А това означава

Пример 3Намерете обема на тялото, ограничен от:

x 2 +y 2 +z 2 =8,

Имаме: x 2 +y 2 +z 2 =8 - сфера с радиус R= v8 с център в точка O(000),

Горната част на конуса z 2 =x 2 +y 2 с оста на симетрия Oz и върха в точка O (фиг. 2.20).

Нека намерим пресечната линия на сферата и конуса:

И тъй като според условието z? 0, тогава

Окръжност R=2, лежаща в равнината z=2.

Следователно, съгласно (2.28)

където областта U е ограничена отгоре

(част от сферата),

(част от конус);

област U се проектира върху равнината Oxy в област D - кръг с радиус 2.

Следователно е препоръчително да се премине към цилиндрични координати в тройния интеграл, като се използват формули (2.36):

Границите на изменение q, r се намират в областта D v на пълната окръжност R = 2 с център в точка O, при което: 0?q?2р, 0?r?2. Така областта U в цилиндрични координати се дава от следните неравенства: