Hogyan kell megoldani egy egyenletet az 5. hatványra. Magasabb fokú egyenletek

Mérlegeljük a másodiknál egy fokozattal magasabb változójú egyenletek megoldása.

A P(x) = 0 egyenlet foka a P(x) polinom foka, azaz. tagjának legnagyobb hatványa, amelynek együtthatója nem egyenlő nullával.

Így például az (x 3 – 1) 2 + x 5 = x 6 – 2 egyenletnek van ötödik foka, mert a zárójelek felnyitásának és hasonlók hozásának műveletei után megkapjuk az x 5 – 2x 3 + 3 = 0 ötödfokú egyenletet.

Idézzük fel azokat a szabályokat, amelyekre szükség lesz kettőnél nagyobb fokú egyenletek megoldásához.

Állítások a polinom gyökereiről és osztóiról:

1. Polinom n-edik fokozat gyökeinek száma nem haladja meg az n-t, és az m többszörösségű gyökök pontosan m-szer fordulnak elő.

2. A páratlan fokú polinomnak legalább egy valós gyöke van.

3. Ha α a P(x) gyöke, akkor P n (x) = (x – α) · Q n – 1 (x), ahol Q n – 1 (x) egy (n – 1) fokú polinom. .

5. Az egész együtthatós redukált polinomnak nem lehet tört racionális gyöke.

6. Harmadfokú polinomhoz

P 3 (x) = ax 3 + bx 2 + cx + d két dolog egyike lehetséges: vagy három binomiális szorzatára bontjuk

Р 3 (x) = а(х – α)(х – β)(х – γ), vagy felbomlik egy binomiális és másodfokú trinomikus P 3 (x) = a(x – α)(x 2 + βx + γ).

7. Bármely negyedfokú polinom kiterjeszthető két négyzetháromtag szorzatára.

8. Egy f(x) polinom maradék nélkül osztható egy g(x) polinommal, ha van olyan q(x) polinom, hogy f(x) = g(x) · q(x). A polinomok felosztására a „sarokosztás” szabályt használjuk.

9. Ahhoz, hogy a P(x) polinom osztható legyen egy binomimmal (x – c), szükséges és elegendő, hogy a c szám legyen P(x) gyöke (Bezout tételének következménye).

10. Vieta tétele: Ha x 1, x 2, ..., x n a polinom valós gyökei

P(x) = a 0 x n + a 1 x n - 1 + ... + a n, akkor a következő egyenlőségek teljesülnek:

x 1 + x 2 + … + x n = -a 1 /a 0,

x 1 x 2 + x 1 x 3 + … + x n – 1 x n = a 2 /a 0,

x 1 x 2 x 3 + … + x n – 2 x n – 1 x n = -a 3 / a 0,

x 1 · x 2 · x 3 · x n = (-1) n a n / a 0 .

Megoldási példák

1. példa

Határozzuk meg a P(x) = x 3 + 2/3 x 2 – 1/9 osztás maradékát (x – 1/3-al).

Megoldás.

Bezout tételének következményeként: „Egy polinom maradéka binomimmal osztva (x – c) egyenlő c polinomjának értékével.” Határozzuk meg, hogy P(1/3) = 0. Ezért a maradék 0, és az 1/3 szám a polinom gyöke.

Válasz: R = 0.

2. példa

Ossza el egy „sarokkal” 2x 3 + 3x 2 – 2x + 3 (x + 2) értékkel. Keresse meg a maradék és a hiányos hányadost.

Megoldás:

2x 3 + 3x 2 – 2x + 3| x + 2

2x 3 + 4 x 2 2x 2 – x

X 2-2 x

Válasz: R = 3; hányados: 2x 2 – x.

A magasabb fokú egyenletek megoldásának alapvető módszerei

1. Új változó bevezetése

Az új változó bevezetésének módja már ismerős a bikvadratikus egyenletek példájából. Abból áll, hogy az f(x) = 0 egyenlet megoldásához egy új változót (helyettesítés) t = x n vagy t = g(x) vezetünk be, és f(x)-t t-n keresztül fejezzük ki, így egy új r egyenletet kapunk. (t). Ezután az r(t) egyenletet megoldva megtaláljuk a gyököket:

(t 1, t 2, …, t n). Ezek után kapunk egy n egyenlethalmazt q(x) = t 1, q(x) = t 2, … , q(x) = t n, amelyből az eredeti egyenlet gyökerei találhatók.

1. példa

(x 2 + x + 1) 2 – 3 x 2 – 3 x – 1 = 0.

Megoldás:

(x 2 + x + 1) 2 – 3 (x 2 + x) – 1 = 0.

(x 2 + x + 1) 2 – 3 (x 2 + x + 1) + 3 – 1 = 0.

Behelyettesítés (x 2 + x + 1) = t.

t 2 – 3t + 2 = 0.

t 1 = 2, t 2 = 1. Fordított helyettesítés:

x 2 + x + 1 = 2 vagy x 2 + x + 1 = 1;

x 2 + x - 1 = 0 vagy x 2 + x = 0;

Válasz: Az első egyenletből: x 1, 2 = (-1 ± √5)/2, a másodikból: 0 és -1.

2. Faktorizálás csoportosítással és rövidített szorzóképletekkel

Ennek a módszernek az alapja sem új, és a kifejezések olyan csoportosításából áll, amelyet minden csoport tartalmaz közös szorzó. Ehhez néha szükség van bizonyos mesterséges technikák alkalmazására.

1. példa

x 4 – 3x 2 + 4x – 3 = 0.

Megoldás.

Képzeljük el - 3x 2 = -2x 2 - x 2 és csoportosítsuk:

(x 4 – 2x 2) – (x 2 – 4x + 3) = 0.

(x 4 – 2x 2 +1 – 1) – (x 2 – 4x + 3 + 1 – 1) = 0.

(x 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.

(x 2 – 1) 2 – (x – 2) 2 = 0.

(x 2 – 1 – x + 2) (x 2 – 1 + x – 2) = 0.

(x 2 – x + 1) (x 2 + x – 3) = 0.

x 2 – x + 1 = 0 vagy x 2 + x – 3 = 0.

Válasz: Az első egyenletben nincs gyök, a másodiktól kezdve: x 1, 2 = (-1 ± √13)/2.

3. Faktorizálás meghatározatlan együtthatók módszerével

A módszer lényege, hogy az eredeti polinomot ismeretlen együtthatókkal faktorizáljuk. Azt a tulajdonságot felhasználva, hogy a polinomok egyenlőek, ha az együtthatójuk azonos hatványokra egyenlő, az ismeretlen bővítési együtthatókat megtaláljuk.

1. példa

x 3 + 4x 2 + 5x + 2 = 0.

Megoldás.

Egy 3-as fokú polinom lineáris és másodfokú tényezők szorzatára bővíthető.

x 3 + 4x 2 + 5x + 2 = (x – a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 +bx 2 + cх – ax 2 – abх – ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b – a)x 2 + (cx – ab)x – ac.

A rendszer megoldása után:

(b – a = 4,
(c – ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, azaz

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

Az (x + 1)(x 2 + 3x + 2) = 0 egyenlet gyökerei könnyen megtalálhatók.

Válasz: -1; -2.

4. A gyökér kiválasztásának módja a legmagasabb és szabad együttható használatával

A módszer a következő tételek alkalmazásán alapul:

1) Az egész együtthatós polinom minden gyöke a szabad tag osztója.

2) Ahhoz, hogy a p/q irreducibilis tört (p - egész szám, q - természetes) legyen egy egész együtthatós egyenlet gyöke, szükséges, hogy a p szám az a 0 szabad tag egész osztója legyen, és q - a vezető együttható természetes osztója.

1. példa

6x 3 + 7x 2 – 9x + 2 = 0.

Megoldás:

6: q = 1, 2, 3, 6.

Ezért p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Ha találtunk egy gyökéröt, például – 2, akkor a sarokosztás, a határozatlan együtthatók módszere vagy a Horner-séma segítségével más gyökereket is találunk.

Válasz: -2; 1/2; 1/3.

Van még kérdése? Nem tudja, hogyan kell egyenleteket megoldani?
Ha segítséget szeretne kérni egy oktatótól, regisztráljon.
Az első óra ingyenes!

weboldalon, az anyag teljes vagy részleges másolásakor a forrásra mutató hivatkozás szükséges.

Osztály: 9

Alapvető célok:

Erősítsd meg a th fokú teljes racionális egyenlet fogalmát.
Fogalmazza meg a magasabb fokú egyenletek megoldásának alapvető módszereit (n > 3).
Tanítsa meg a magasabb rendű egyenletek megoldásának alapvető módszereit.
Megtanítani, hogyan határozzuk meg a legtöbbet hatékony módszer a döntéseit.

A tanár által az osztályteremben alkalmazott formák, módszerek és pedagógiai technikák:

Előadás-szeminárium oktatási rendszer (előadások - új anyag magyarázata, szemináriumok - problémamegoldás).
Információs és kommunikációs technológiák (frontális felmérés, szóbeli munka az osztállyal).
Differenciált tanulási, csoportos és egyéni formák.
Olyan kutatási módszer alkalmazása a tanításban, amely az egyes tanulók matematikai apparátusának és gondolkodási képességének fejlesztését célozza.
Nyomtatott anyag - az óra egyéni rövid összefoglalása (alapfogalmak, képletek, állítások, diagramok vagy táblázatok formájában sűrített előadásanyag).

Tanterv:

Idő szervezése.
A szakasz célja: a tanulók bevonása az oktatási tevékenységekbe, az óra tartalmának meghatározása.
A tanulók tudásának frissítése.
A szakasz célja: a hallgatók ismereteinek frissítése a korábban tanult kapcsolódó témákban
Új téma tanulása (előadás). A szakasz célja: a magasabb fokú egyenletek megoldásának alapvető módszereinek megfogalmazása (n > 3)
Összegzés.
A szakasz célja: ismét kiemelni a leckében tanult anyag legfontosabb pontjait.
Házi feladat.
A színpad célja: megfogalmazni házi feladat diákoknak.

Óra összefoglalója

1. Szervezési mozzanat.

Az óra témájának megfogalmazása: „Magasabb erők egyenletei. Megoldásuk módszerei.”

2. A tanulók tudásának frissítése.

Elméleti felmérés - beszélgetés. Néhány korábban tanulmányozott információ megismétlése az elméletből. A hallgatók megfogalmazzák az alapvető definíciókat és megfogalmazzák a szükséges tételeket. Mondjon példákat a korábban megszerzett tudás szintjének bemutatására!

Egy változós egyenlet fogalma.
Az egyenlet gyökerének fogalma, az egyenlet megoldása.
Koncepció lineáris egyenlet egy változóval, egy változós másodfokú egyenlet fogalma.
Az egyenletek, egyenletek-következmények ekvivalenciájának fogalma (külső gyökök fogalma), nem következmény általi átmenet (gyökvesztés esete).
Egy egész racionális kifejezés fogalma egy változóval.
A teljes racionális egyenlet fogalma n fokozat. Egy egész racionális egyenlet standard alakja. Csökkentett teljes racionális egyenlet.
Áttérés alacsonyabb fokú egyenlethalmazra az eredeti egyenlet faktorálásával.
A polinom fogalma n fokozattól x. Bezout tétele. Következtetések Bezout tételéből. Gyöktételek ( Z-gyökerek és K-gyökei) egy egész racionális egyenlet egész együtthatóival (redukált és redukálatlan).
Horner séma.

3. Új téma tanulmányozása.

Az egész racionális egyenletet figyelembe vesszük n-a szabványos alak hatványa egy ismeretlen változóval x:Pn(x)= 0, ahol P n (x) = a n x n + a n-1 x n-1 + a 1 x + a 0– polinom n fokozattól x, a n ≠ 0. Ha a n = 1, akkor az ilyen egyenletet redukált egész számú racionális egyenletnek nevezzük n fokozat. Tekintsük az ilyen egyenleteket különböző jelentések nés sorolja fel a megoldásukra szolgáló főbb módszereket.

n= 1 – lineáris egyenlet.

n = 2 – másodfokú egyenlet. Diszkrimináns képlet. Képlet a gyökerek kiszámításához. Vieta tétele. Egy teljes négyzet kiválasztása.

n = 3 – köbös egyenlet.

Csoportosítási módszer.

Példa: x 3 – 4x 2 – x+ 4 = 0 (x – 4) (x 2– 1) = 0 x 1 = 4 , x 2 = 1,x 3 = -1.

A forma reciprok köbegyenlete fejsze 3 + bx 2 + bx + a= 0. Azonos együtthatójú tagok kombinálásával oldjuk meg.

Példa: x 3 – 5x 2 – 5x + 1 = 0 (x + 1)(x 2 – 6x + 1) = 0 x 1 = -1, x 2 = 3 + 2, x 3 = 3 – 2.

Z-gyökök kiválasztása a tétel alapján. Horner séma. A módszer alkalmazásakor hangsúlyozni kell, hogy a keresés ebben az esetben véges, és a gyököket egy bizonyos algoritmussal választjuk ki a kb. tételnek megfelelően. Z-az adott egész racionális egyenlet gyökei egész együtthatókkal.

Példa: x 3 – 9x 2 + 23x– 15 = 0. Az egyenlet adott. Írjuk fel a szabad tag osztóit ( + 1; + 3; + 5; + 15). Alkalmazzuk Horner sémáját:

	x 3	x 2	x 1	x 0	következtetés
	1	-9	23	-15
1	1	1 x 1 – 9 = -8	1 x (-8) + 23 = 15	1 x 15 – 15 = 0	1 – gyökér
	x 2	x 1	x 0

Kapunk ( x – 1)(x 2 – 8x + 15) = 0 x 1 = 1, x 2 = 3, x 3 = 5.

Egyenlet egész együtthatókkal. Q-gyökök kiválasztása a tétel alapján. Horner séma. A módszer alkalmazásakor hangsúlyozni kell, hogy a keresés ebben az esetben véges, és a gyököket egy bizonyos algoritmussal választjuk ki a kb. tételnek megfelelően. K-egy redukálatlan egész számú racionális egyenlet gyökei egész együtthatókkal.

Példa: 9 x 3 + 27x 2 – x– 3 = 0. Az egyenlet redukálatlan. Írjuk fel a szabad tag osztóit ( + 1; + 3). Írjuk fel az együttható osztóit az ismeretlen legmagasabb hatványán. ( + 1; + 3; + 9) Következésképpen gyökereket fogunk keresni az értékek között ( + 1; + ; + ; + 3). Alkalmazzuk Horner sémáját:

	x 3	x 2	x 1	x 0	következtetés
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 – 1 = 35	1 x 35 – 3 = 32 ≠ 0	1 – nem gyökér
-1	9	-1 x 9 + 27 = 18	-1 x 18 – 1 = -19	-1 x (-19) – 3 = 16 ≠ 0	-1 – nem gyökér
	9	x 9 + 27 = 30	x 30 – 1 = 9	x 9 – 3 = 0	gyökér
	x 2	x 1	x 0

Kapunk ( x – )(9x 2 + 30x + 9) = 0 x 1 = , x 2 = - , x 3 = -3.

A számítás megkönnyítése érdekében a Q kiválasztásakor -gyökerek Kényelmes lehet a változó megváltoztatása, lépjen az adott egyenletre, és válassza a Z-t -gyökerek.

Ha az áltag 1

.

Ha használhatja az űrlap helyettesítését y = kx

.

Cardano formula. Van egy univerzális módszer a köbös egyenletek megoldására - ez a Cardano képlet. Ez a képlet Gerolamo Cardano (1501–1576), Nicolo Tartaglia (1500–1557) és Scipione del Ferro (1465–1526) olasz matematikusok nevéhez fűződik. Ez a képlet túlmutat tanfolyamunk keretein.

n= 4 – a negyedik fokozat egyenlete.

Csoportosítási módszer.

Példa: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 (x 4 + 2x 3) + (5x 2 + 10x) – (6x + 12) = 0 (x + 2)(x 3 + 5x - 6) = 0 (x + 2)(x– 1)(x 2 + x + 6) = 0 x 1 = -2, x 2 = 1.

Változó helyettesítési módszer.

Az alak kétnegyedes egyenlete fejsze 4 + bx 2 + s = 0 .

Példa: x 4 + 5x 2 – 36 = 0. Csere y = x 2. Innen y 1 = 4, y 2 = -9. Ezért x 1,2 = + 2 .

Az alak negyedik fokának reciprok egyenlete fejsze 4 + bx 3+c x 2 + bx + a = 0.

Úgy oldjuk meg, hogy azonos együtthatójú tagokat kombinálunk az űrlap helyettesítésével

fejsze 4 + bx 3 + cx 2 – bx + a = 0.

A forma negyedik fokának általánosított ismétlődő egyenlete fejsze 4 + bx 3 + cx 2 + kbx + k 2 a = 0.

Általános csere. Néhány szabványos csere.

3. példa . Általános nézet csere(a fajlagos egyenlet típusából következik).

n = 3.

Egyenlet egész együtthatókkal. Q-gyökök kiválasztása n = 3.

Általános képlet. Van egy univerzális módszer a negyedfokú egyenletek megoldására. Ez a képlet Ludovico Ferrari (1522–1565) nevéhez fűződik. Ez a képlet túlmutat tanfolyamunk keretein.

n > 5 – ötödik és magasabb fokozatú egyenletek.

Egyenlet egész együtthatókkal. Z-gyökök kiválasztása a tétel alapján. Horner séma. Az algoritmus hasonló a fentebb tárgyalthoz n = 3.

Egyenlet egész együtthatókkal. Q-gyökök kiválasztása tétel alapján. Horner séma. Az algoritmus hasonló a fentebb tárgyalthoz n = 3.

Szimmetrikus egyenletek. Minden páratlan fokú reciprok egyenletnek van gyöke x= -1, és faktorokká való faktorálás után azt kapjuk, hogy az egyik faktor alakja ( x+ 1), a második tényező pedig egy páros fokú reciprok egyenlet (fokozata eggyel kisebb, mint az eredeti egyenlet mértéke). Bármely páros fokú reciprok egyenlet az alak gyökével együtt x = φ tartalmazza a faj gyökerét is. Ezeket az állításokat felhasználva a problémát a vizsgált egyenlet mértékének csökkentésével oldjuk meg.

Változó helyettesítési módszer. A homogenitás használata.

Nincs általános képlet az ötödik fokú teljes egyenletek megoldására (ezt Paolo Ruffini (1765–1822) olasz matematikus és Niels Henrik Abel (1802–1829) norvég matematikus mutatta meg) és a magasabb fokozatok (ezt a francia matematikus, Evariste Galois (1811–1832) )).

Emlékezzünk még egyszer arra, hogy a gyakorlatban is lehet használni kombinációk a fent felsorolt módszereket. Kényelmes áttérni az alacsonyabb fokú egyenletekre az eredeti egyenlet faktorálása.
Mai vita tárgyain kívül esnek azok, amelyeket a gyakorlatban széles körben használnak. grafikus módszerek egyenletek megoldása és közelítő megoldási módszerek magasabb fokú egyenletek.

Vannak helyzetek, amikor az egyenletnek nincs R-gyöke.

A függvények monotonitásának tulajdonságának felhasználása

4. Összegzés.

Összegzés: Mostanra elsajátítottuk a különféle magasabb fokú egyenletek megoldásának alapvető módszereit (n. > 3). Feladatunk a fent felsorolt algoritmusok hatékony használatának elsajátítása. Az egyenlet típusától függően meg kell tanulnunk meghatározni, hogy adott esetben melyik megoldás a leghatékonyabb, valamint a választott módszert helyesen alkalmazni.

5. Házi feladat.

: 7. bekezdés, 164–174., 33–36., 39–44., 46.47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Lehetséges témakörök a témával kapcsolatos riportokhoz vagy absztraktokhoz:

Cardano formula
Grafikus módszer egyenletek megoldására. Példák megoldásokra.
Egyenletek közelítő megoldásának módszerei.

A tanulók tanulásának és a téma iránti érdeklődésének elemzése:

A tapasztalatok azt mutatják, hogy a tanulók érdeklődését elsősorban a válogatás lehetősége kelti fel Z-gyökerek és K-egyenletek gyökerei egy meglehetősen egyszerű algoritmus segítségével, Horner sémáját használva. A tanulókat érdeklik a változók különféle szabványos helyettesítési típusai is, amelyek jelentősen leegyszerűsíthetik a probléma típusát. A grafikus megoldási módszerek általában különösen érdekesek. Ebben az esetben a problémákat egyenletek megoldására szolgáló grafikus módszerrel is elemezheti; megbeszélni általános forma grafika 3, 4, 5 fokos polinomokhoz; elemezze, hogy a 3, 4, 5 fokú egyenletek gyökeinek száma hogyan függ össze a megfelelő gráf megjelenésével. Az alábbiakban felsoroljuk azokat a könyveket, amelyekben további információkat találhat erről a témáról.

Bibliográfia:

Vilenkin N.Ya.és mások „Algebra. Tankönyv 9. osztályos tanulók számára a matematika elmélyült tanulmányozásával” - M., Prosveshchenie, 2007 - 367 p.
Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.„Egy matematika tankönyv lapjai mögött. Számtan. Algebra. 10-11 évfolyam” – M., Oktatás, 2008 – 192 p.
Vygodsky M.Ya.„Matematika kézikönyve” – M., AST, 2010 – 1055 p.
Galitsky M.L.„Feladatok gyűjtése az algebrában. oktatóanyag a 8-9. osztály számára a matematika elmélyült tanulmányozásával” - M., Prosveshchenie, 2008 - 301 p.
Zvavich L.I.és mások „Algebra és az elemzés kezdetei. 8-11 évfolyam Kézikönyv iskolák és osztályok számára, ahol haladó szintű matematikai tanulmányokat folytatnak” - M., Bustard, 1999 - 352 p.
Zvavich L.I., Averyanov D.I., Pigarev B.P., Trushanina T.N.„Matematikai feladatok az írásbeli vizsgára való felkészüléshez a 9. osztályban” - M., Prosveshchenie, 2007 - 112 p.
Ivanov A.A., Ivanov A.P.„Tematikus tesztek a matematikai ismeretek rendszerezéséhez” 1. rész – M., Fizmatkniga, 2006 – 176 p.
Ivanov A.A., Ivanov A.P.„Tematikus tesztek a matematikai ismeretek rendszerezéséhez” 2. rész – M., Fizmatkniga, 2006 – 176 p.
Ivanov A.P.„Tesztek és tesztek a matematikában. Oktatóanyag". – M., Fizmatkniga, 2008 – 304 p.
Leibson K.L.„Gyakorlati feladatok gyűjteménye matematikából. rész 2–9 évfolyam” – M., MCNMO, 2009 – 184 p.
Makarychev Yu.N., Mindyuk N.G."Algebra. További fejezetek a 9. osztályos iskolai tankönyvhöz. Tankönyv az iskolák és osztályok tanulói számára a matematika elmélyült tanulmányozásával.” – M., Oktatás, 2006 – 224 p.
Mordkovich A.G."Algebra. Mélyreható tanulmányozás. 8. osztály. Tankönyv” – M., Mnemosyne, 2006 – 296 p.
Savin A.P. “enciklopédikus szótár fiatal matematikus” - M., Pedagógia, 1985 - 352 p.
Survillo G.S., Simonov A.S.„Didaktikai anyagok az algebráról a 9. osztály számára a matematika elmélyült tanulmányozásával” - M., Prosveshchenie, 2006 - 95 p.
Chulkov P.V.„Egyenletek és egyenlőtlenségek az iskolai matematika kurzusban. Előadások 1–4” – M., 2006. szeptember 1. – 88 p.
Chulkov P.V.„Egyenletek és egyenlőtlenségek az iskolai matematika kurzusban. Előadások 5–8” – M., 2009. szeptember 1. – 84 p.

A 16. században a matematikusok szinte véletlenül botlottak összetett számokba (lásd a 11. fejezetet). NAK NEK XVIII század a komplex számokat a régió kiterjesztésének tekintették valós számok, de a velük való munka így is paritáshibához vezetett, mivel Leonard E. számelméleti nagy művében, az Aritmikai vizsgálatokban (1801) kerülte az úgynevezett „képzetes számok” használatát. Számomra úgy tűnik, hogy ennek a munkának a legfontosabb része az algebra alaptételének első bizonyítása. Gauss felismerte ennek a tételnek a fontosságát, és a következő években több további bizonyítást is készített. 1849-ben átdolgozta az első változatot, ezúttal összetett számokkal. Kihasználva modern kifejezéssel, azt mondhatjuk, hogy bármely valós vagy összetett együtthatójú véges polinomegyenletnek minden gyöke valós, ill. komplex számok. Így nemleges választ kapunk arra a régóta fennálló kérdésre, hogy a polinomiális egyenletek megoldásához szükséges-e magasrendű a komplexeknél magasabb rendű számok létrehozása.

Az akkori algebra egyik legkínosabb problémája az volt, hogy az ötödrendű polinom, a kvintikus megoldható-e algebrai módszerekkel, azaz véges számú algebrai lépéssel. Napjainkban az iskolában a másodfokú egyenletek megoldásának képletét tanítják, a 16. század óta ismertek hasonló módszerek a harmad- és negyedfokú egyenletek megoldására is (11. fejezet). De nem találtak egyetlen módszert sem a kvintikára. Az algebra alaptétele látszólag pozitív válasz reményében rejlik, de valójában egyszerűen a megoldások létezését garantálja, nem mond semmit a pontos megoldásokat adó képletek létezéséről (akkor már léteztek hozzávetőleges numerikus és grafikus módszerek ). És ekkor megjelent két tragikus sorsú matematikai zseni.

Niels Henrik Abel (1802–1829) egy nagy, szegény családban született egy kis faluban Norvégiában, egy országban, amelyet az Angliával és Svédországgal vívott hosszú évek háborúja pusztított el. A fiúval kedveskedő tanárnő magánórákat adott neki, de édesapja halála után, tizennyolc évesen, fiatal kora és törékeny egészsége ellenére Ábel kénytelen volt eltartani a családját. 1824-ben publikált egy tudományos cikket, amelyben kijelentette, hogy a quintic nem oldható meg algebrai eszközökkel, mint ahogy minden magasabb rendű polinom sem. Abel úgy gondolta, hogy ez a cikk lesz a jegye a tudományos világba, és elküldte Gaussnak a Göttingeni Egyetemre. Sajnos Gauss soha nem vágta a lapokat késsel (akkoriban minden olvasónak meg kellett tennie), és nem olvasta el a cikket. 1826-ban a norvég kormány végre pénzeszközöket biztosított Ábelnek, hogy Európa körül utazhasson. Attól tartva, hogy a Gauss-szal folytatott személyes kommunikáció nem okoz neki sok örömet, a matematikus úgy döntött, nem látogat el Göttingenbe, hanem Berlinbe ment. Ott kötött barátságot August Leopold Krelle-lel (1780–1855), matematikussal, építészsel és mérnökkel, aki matematikai kérdésekben tanácsot adott a Porosz Oktatási Minisztériumnak. Krell szándékában állt megalapítani a Journal of Pure and Applied Mathematics-t. Így Ábel lehetőséget kapott munkáinak terjesztésére, és sokat publikált, különösen a Journal korai számaiban, amelyet azonnal igen tekintélyes és tekintélyes tudományos publikációnak kezdtek tekinteni. A norvég közzétette ott annak a bizonyítékának kiterjesztett változatát, hogy a kvintikus algebrai módszerekkel eldönthetetlen. Aztán elment Párizsba. Ez az utazás nagyon felzaklatta Ábelt, mert gyakorlatilag nem kapta meg a szükséges támogatást a francia matematikusoktól. Közel állt hozzá Augustin Louis Cauchy-hoz (1789–1857), aki akkoriban a vezető fényes volt. matematikai elemzés, de nagyon összetett karakterű volt. Ahogy Ábel maga fogalmazott: "Cauchy őrült, és nem lehet ellene tenni semmit, bár jelenleg ő az egyetlen, aki bármire képes a matematikában." Ha megpróbáljuk igazolni a Gauss és Cauchy által kiváltott tiszteletlenség és elhanyagolás megnyilvánulásait, akkor azt mondhatjuk, hogy a quintic bizonyos hírnevet szerzett, és felkeltette mind a tekintélyes matematikusok, mind az originalisták figyelmét. Ábel visszatért Norvégiába, ahol egyre gyakrabban szenvedett tuberkulózisban. Továbbra is küldte munkáját Crelle-nek, de 1829-ben meghalt, nem tudván, hogy hírneve mennyire megszilárdult a tudományos világban. Két nappal halála után Ábel ajánlatot kapott, hogy Berlinben tudományos állást foglaljon el.

Ábel megmutatta, hogy a negyedrend feletti polinomok nem oldhatók meg gyökök, például négyzetgyök, kockagyök vagy magasabb rendű gyök segítségével. Az explicit feltételeket, amelyek mellett speciális esetekben ezek a polinomok megoldhatók, és a megoldási módot Galois fogalmazta meg. Évariste Galois (1811–1832) rövid és eseménydús életet élt. Hihetetlenül tehetséges matematikus volt. Galois könyörtelen volt azokkal szemben, akiket nála kevésbé tartott tehetségesnek, ugyanakkor gyűlölte a társadalmi igazságtalanságot. Nem mutatott rátermettséget a matematikára, amíg el nem olvasta Legendre Geometria elemei című művét (1794-ben jelent meg, ez a könyv volt a következő száz év fő tankönyve). Aztán szó szerint felfalta Legendre és később Ábel többi művét. Lelkesedése, önbizalma és intoleranciája vezetett igazán szőrnyű következmények tanárokkal és vizsgáztatókkal való kapcsolatában. Galois részt vett a francia matematika bölcsőjébe, az École Polytechnique-re kiírt versenyen, de felkészültség hiányában megbukott a vizsgán. Miután megismerkedett egy új tanárral, aki felismerte tehetségét, egy ideig sikerült kordában tartania az indulatait. Galois 1829 márciusában publikálta első dolgozatát a tört folytatásról, amelyet legjelentősebb munkájának tartott. Felfedezéseiről üzenetet küldött a Tudományos Akadémiának, Cauchy megígérte, hogy bemutatja őket, de elfelejtette. Ráadásul egyszerűen elvesztette a kéziratot.

Galois második kudarca, hogy belépjen az École Polytechnique-be, a matematikai folklór részévé vált. Annyira hozzászokott ahhoz, hogy állandóan bonyolult matematikai gondolatokat tartson a fejében, hogy feldühítette a vizsgáztatók kicsinyes nyavalygása. Mivel a vizsgáztatók nehezen értették meg a magyarázatát, a tábláról egy száraz törlőruhát dobott egyikük arcába. Nem sokkal ezután apja meghalt, és az egyházi intrikák következtében öngyilkos lett. Gyakorlatilag lázadás tört ki a temetésén. 1830 februárjában Galois megírta a következő három dolgozatot, és elküldte azokat a Tudományos Akadémiának a matematikai nagydíjra. Joseph Fourier, az akadémia akkori titkára anélkül halt meg, hogy elolvasta őket, és halála után a cikkeket nem találták meg iratai között. A csalódás ekkora áradata bárkit úrrá lett volna. Galois fellázadt a hatalmon lévők ellen, mert úgy érezte, hogy nem ismerik el érdemeit, és megsemmisítette apját. Határozottan belevetette magát a politikába, és lelkes köztársaságpárti lett – nem a legbölcsebb döntés Franciaországban 1830-ban. Utolsó kísérletként tudományos dolgozatot küldött a híres francia fizikusnak és matematikusnak, Simeon Denis Poissonnak (1781–1840), aki válaszul további bizonyítékokat követelt.

Azzá vált az utolsó csepp. 1831-ben Galois-t kétszer is letartóztatták – először azért, mert állítólag Lajos Fülöp király meggyilkolására szólított fel, majd a védelme érdekében – a hatóságok a köztársasági lázadástól tartottak! Ezúttal hat hónap börtönbüntetésre ítélték koholt vádak miatt, mert illegálisan viselte a feloszlatott tüzér zászlóalj egyenruháját, amelyhez csatlakozott. Feltételesen szabadlábra helyezve olyan feladatot vállalt, amitől éppúgy undorodtak, mint minden mástól az életben. Odaadó barátjának, Chevalier-nek írt leveleiben érezhető csalódottsága. 1832. május 29-én elfogadta a kihívást egy párbajra, amelynek okait nem teljesen értik. „Egy becstelen kacérkodás áldozata lettem. Az életem kialudt egy nyomorúságos veszekedésben” – írja a „Level minden republikánusnak” című könyvében. Galois leghíresebb művét a végzetes párbaj előtti éjszakán vázolták fel. A margón elszórtan vannak panaszok: „Nincs már időm, nincs már időm.” Kénytelen volt másokra bízni azoknak a köztes lépéseknek a részletes ismertetését, amelyek nem voltak elengedhetetlenek a fő gondolat megértéséhez. Papírra kellett vetnie felfedezései alapját – a ma Galois-tételnek nevezett tétel eredetét. Végrendeletét azzal fejezte be, hogy felkérte Chevalier-t, hogy "kérje meg Jacobit és Gausst, hogy mondják el közvéleményüket, nem a tételek helyességét, hanem fontosságát illetően". Kora reggel Galois elment, hogy találkozzon riválisával. 25 lépés távolságból kellett lőniük. Galois megsebesült, és másnap reggel a kórházban meghalt. Még csak húsz éves volt.

Galois Lagrange és Cauchy munkáira épített, de többet fejlesztett általános módszer. Ez rendkívül fontos eredmény volt a kvintika megoldása terén. A tudós kevesebb figyelmet fordított az eredeti egyenletekre vagy a grafikus értelmezésre, és többet gondolt magukra a gyökerek természetére. Az egyszerűsítés kedvéért Galois csak az úgynevezett irreducibilis kvintikákat vette figyelembe, vagyis azokat, amelyek nem faktorizálhatók alacsonyabb rendű polinomok formájában (amint mondtuk, a negyedrendű polinomegyenletekhez vannak képletek, amelyekkel megtalálhatjuk a polinomokat. gyökerei). Egyáltalán irreducibilis polinom A racionális együtthatókkal olyan polinom, amely nem bővíthető egyszerűbb, racionális együtthatós polinomokra. Például (x 5 - 1) faktorizálható (x-1) (x 4 + x 3 + x 2 + x + 1), mivel (x 5-2) nem csökkenthető. Galois célja az volt, hogy meghatározza azokat a feltételeket, amelyek mellett egy általános irreducibilis polinomegyenlet összes megoldása megtalálható gyökökben.

A megoldás kulcsa, hogy egyetlen irreducibilis algebrai egyenlet gyökei nem függetlenek, egymáson keresztül kifejezhetők. Ezeket a relációkat az összes lehetséges permutáció csoportjába, az úgynevezett gyökszimmetria csoportba formalizálták - egy kvintikus esetében ez a csoport 5-öt tartalmaz! = 5 x 4 x 3 x 2 x 1 = 120 elem. A Galois-elmélet matematikai algoritmusai nagyon összetettek, és valószínűleg részben ennek köszönhetően kezdetben nehezen érthetőek voltak. De miután az absztrakció szintje lehetővé tette, hogy elmozduljunk algebrai megoldások egyenletek algebrai szerkezet asszociált csoportokat, Galois meg tudta jósolni az egyenlet megoldhatóságát az ilyen csoportok tulajdonságai alapján. Sőt, elmélete egy olyan módszert is adott, amellyel ezek a gyökerek maguk is fellelhetők. Ami a kvintikat illeti, Joseph Liouville (1809–1882) matematikus, aki 1846-ban Galois munkájának nagy részét publikálta a Journal of Pure and Applied Mathematics című folyóiratban, megjegyezte, hogy a fiatal tudós „szép tételt” bizonyított, és hogy „hogy Ha egy eredeti fokú irreducibilis egyenlet megoldható gyökökben, akkor szükséges és elégséges, hogy minden gyöke racionális függvények bármelyik kettő." Mivel ez egy kvintikus számára lehetetlen, nem oldható meg gyökök segítségével.

Három év alatt a matematikai világ két legfényesebb új csillagát veszítette el. Kölcsönös vádaskodás és lélekkutatás következett, Abel és Galois pedig megérdemelt elismerést ért el, de csak posztumusz. 1829-ben Carl Jacobi Legendre útján szerzett tudomást Ábel „elveszett” kéziratáról, 1830-ban pedig diplomáciai botrány robbant ki, amikor a párizsi norvég konzul követelte honfitársa cikkének megtalálását. Cauchy végül megtalálta a cikket, de az akadémia szerkesztői újra elvesztették! Ugyanebben az évben Ábel elnyerte a Matematikai Grand Prix-t (Jacobival megosztva) – de már halott volt. 1841-ben jelent meg életrajza. 1846-ban Liouville megszerkesztette Galois néhány kéziratát publikálás céljából, és a bevezetőben sajnálatát fejezte ki amiatt, hogy az akadémia kezdetben elutasította Galois munkáját annak összetettsége miatt – „a bemutatás egyértelműségére valóban szükség van, ha a szerző levezeti az olvasót a kitaposott ösvényről a feltérképezetlen vadonba. területeken." Így folytatja: „Galois nincs többé! Ne essünk haszontalan kritikákba. Tegyük félre a hiányosságokat, és nézzük az előnyöket! Gyümölcs rövid élet Galois mindössze hatvan oldalba fér bele. Az École Normale és az École Polytechnique jelöltjei számára készült matematikai folyóirat szerkesztője a következőképpen kommentálta a Galois-ügyet: „A magas intelligenciájú jelöltet egy alacsonyabb gondolkodású vizsgáztató kizárta. Barbarus hic ego sum, quia non intelligor illis."

Először is, e mű második oldalát nem terhelik nevek, vezetéknevek, társadalmi státuszleírások, címek és elégiák valami fukar fejedelem tiszteletére, akinek e tömjén segítségével - bezárással fenyegetve - felnyílik a pénztárcája. amikor a dicséret véget ér. Nem fogsz itt látni áhítatos laudációkat, amelyek háromszor nagyobb betűkkel vannak írva, mint maga a szöveg, és amelyek a tudományban magas rangúaknak szólnak, valami bölcs mecénásnak – ami kötelező (mondanám elkerülhetetlen) annak, aki húsz évesen akar. írni valamit. Nem mondom el itt senkinek, hogy tartozom tanácsaikkal és támogatásukkal minden jóért, ami a munkámból származik. Ezt nem azért mondom, mert hazugság lenne. Ha megemlíteném a társadalom vagy a tudomány egyik nagyságát (a két emberosztály közötti különbség jelenleg szinte észrevehetetlen), esküszöm, hogy nem a hála jele lenne. Nekik köszönhetem, hogy e két cikk közül az elsőt ilyen későn publikáltam, és hogy mindezt a börtönben írtam - egy olyan helyen, amely aligha tekinthető alkalmasnak tudományos reflexióra, és gyakran elcsodálkozom visszafogottságomon és tartási képességemen. becsukta a számat a hülye és gonosz zoilokkal kapcsolatban. Azt hiszem, használhatom a "zoiles" szót anélkül, hogy félnék attól, hogy helytelenséggel vádolnak, mivel én így hívom az ellenfeleimet. Nem fogok itt írni arról, hogyan és miért kerültem börtönbe, de azt kell mondanom, hogy kézirataim gyakrabban vesztek el az akadémia úri tagjainak aktáiban, bár igazából ezt el sem tudom képzelni. tapintatlanság az Ábel haláláért felelős emberek részéről. Véleményem szerint bárki szeretne összehasonlítani ezzel a zseniális matematikussal. Elég, ha csak annyit mondok, hogy az egyenletelméletről szóló cikkemet 1830 februárjában küldték el a Tudományos Akadémiának, 1829 februárjában küldtek ki belőle kivonatokat, de ezekből semmit sem nyomtattak ki, sőt a kézirat is lehetetlennek bizonyult. Visszatérés.

Galois, kiadatlan előszó, 1832

BAN BEN általános eset 4-nél nagyobb fokú egyenlet nem oldható meg gyökökben. De néha még mindig megtalálhatjuk egy bal oldali polinom gyökét egy legmagasabb fokú egyenletben, ha polinomok szorzataként ábrázoljuk 4-nél nem nagyobb mértékben. Az ilyen egyenletek megoldása egy polinom faktorálásán alapul, ezért javasoljuk, hogy tekintse át ezt a témát a cikk tanulmányozása előtt.

Leggyakrabban magasabb fokú, egész együtthatós egyenletekkel kell foglalkozni. Ilyen esetekben megpróbálhatjuk megtalálni racionális gyökerei, majd faktorálja a polinomot, hogy ezután egy könnyen megoldható alacsonyabb fokú egyenletté alakíthassa. Ebben az anyagban csak ilyen példákat fogunk megvizsgálni.

Magasabb fokú egyenletek egész együtthatókkal

Az összes egyenlet a n x n + a n - 1 x n - 1 + alakú. . . + a 1 x + a 0 = 0, akkor ugyanolyan fokú egyenletet állíthatunk elő, ha mindkét oldalt megszorozzuk a n n - 1-gyel, és változó változtatást végzünk y = a n x alakban:

a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n - 1 · a n n - 1 · x n - 1 + … + a 1 · (a n) n - 1 · x + a 0 · (a n) n - 1 = 0 y = a n x ⇒ y n + b n - 1 y n - 1 + … + b 1 y + b 0 = 0

Az így kapott együtthatók is egész számok lesznek. Így az n-edik fokú redukált egyenletet egész együtthatókkal kell megoldanunk, amelynek alakja x n + a n x n - 1 + ... + a 1 x + a 0 = 0.

Kiszámoljuk az egyenlet egész gyökét. Ha az egyenletnek egész gyökei vannak, akkor ezeket az a 0 szabad tag osztói között kell keresni. Jegyezzük fel és cseréljük be az eredeti egyenlőségbe egyenként, ellenőrizve az eredményt. Miután megkaptuk az azonosságot, és megtaláltuk az egyenlet egyik gyökerét, felírhatjuk x - x 1 · P n - 1 (x) = 0 alakban. Itt x 1 az egyenlet gyöke, és P n - 1 (x) az x n + a n x n - 1 + ... + a 1 x + a 0 hányadosa osztva x - x 1 -gyel.

A fennmaradó, P n - 1 (x) = 0-ba írt osztókat x 1-gyel kezdve helyettesítjük, mivel a gyökök megismételhetők. Az azonosság megszerzése után az x 2 gyököt találtnak tekintjük, és az egyenlet (x - x 1) (x - x 2) · P n - 2 (x) = 0 alakban írható fel. Itt P n - 2 (x) a P n - 1 (x) x - x 2-vel való osztásának hányadosa.

Folytatjuk a válogatást az osztók között. Keressük meg az összes gyököt, és jelöljük a számukat m-vel. Ezek után az eredeti egyenlet a következőképpen ábrázolható: x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0. Itt P n - m (x) egy n - m fokú polinom. A számításokhoz kényelmes a Horner-séma használata.

Ha az eredeti egyenletünknek egész együtthatója van, akkor végül nem kaphatunk törtgyököket.

A P n - m (x) = 0 egyenlethez jutottunk, melynek gyökerei tetszőleges módon megkereshetők. Lehetnek irracionálisak vagy összetettek.

Mutassuk meg egy konkrét példán, hogyan használják ezt a megoldási sémát.

1. példa

Feltétel: keressük meg az x 4 + x 3 + 2 x 2 - x - 3 = 0 egyenlet megoldását.

Megoldás

Kezdjük azzal, hogy megtaláljuk a teljes gyökereket.

Van egy szabad tagunk mínusz hárommal. Osztói 1, -1, 3 és -3. Helyettesítsük be őket az eredeti egyenletbe, és nézzük meg, melyikük adja a kapott azonosságot.

Ha x egyenlő eggyel, akkor 1 4 + 1 3 + 2 1 2 - 1 - 3 = 0, ami azt jelenti, hogy egy lesz a gyök adott egyenlet.

Most osszuk el az x 4 + x 3 + 2 x 2 - x - 3 polinomot (x - 1) egy oszlopban:

Tehát x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Kaptunk egy azonosságot, ami azt jelenti, hogy megtaláltuk az egyenlet másik gyökerét, ami egyenlő -1-gyel.

Osszuk el az x 3 + 2 x 2 + 4 x + 3 polinomot (x + 1) egy oszlopban:

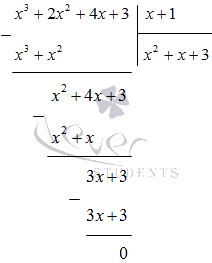
Ezt értjük

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

A következő osztót behelyettesítjük az x 2 + x + 3 = 0 egyenlőségbe, -1-től kezdve:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

A kapott egyenlőségek helytelenek lesznek, ami azt jelenti, hogy az egyenletnek már nincs egész gyöke.

A fennmaradó gyökök az x 2 + x + 3 kifejezés gyökerei lesznek.

D = 1 2 - 4 1 3 = - 11< 0

Ebből következik, hogy ennek a másodfokú trinomnak nincsenek valódi gyökei, de vannak összetett konjugált gyökei: x = - 1 2 ± i 11 2.

Tisztázzuk, hogy oszlopra osztás helyett Horner séma is használható. Ez így történik: miután meghatároztuk az egyenlet első gyökét, kitöltjük a táblázatot.

Az együtthatók táblázatában azonnal láthatjuk a polinomok osztásának hányadosának együtthatóit, ami x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 .

A következő gyökér megtalálása után, amely - 1, a következőket kapjuk:

Válasz: x = - 1, x = 1, x = - 1 2 ± i 11 2.

2. példa

Feltétel: oldja meg az x 4 - x 3 - 5 x 2 + 12 = 0 egyenletet.

Megoldás

A szabad tagnak 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12 osztói vannak.

Nézzük őket sorban:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Ez azt jelenti, hogy x = 2 lesz az egyenlet gyöke. Osszuk el x 4 - x 3 - 5 x 2 + 12 x - 2-vel a Horner-séma szerint:

Ennek eredményeképpen x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

Ez azt jelenti, hogy ismét a 2 lesz a gyökér. Oszd x 3 + x 2 - 3 x - 6 = 0 x - 2-vel:

Ennek eredményeként azt kapjuk, hogy (x - 2) 2 · (x 2 + 3 x + 3) = 0.

A fennmaradó osztók ellenőrzésének nincs értelme, mivel az x 2 + 3 x + 3 = 0 egyenlőség gyorsabb és kényelmesebb a diszkrimináns segítségével megoldani.

Oldjuk meg a másodfokú egyenletet:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Egy komplex konjugált gyökpárt kapunk: x = - 3 2 ± i 3 2 .

Válasz: x = - 3 2 ± i 3 2 .

3. példa

Feltétel: Határozzuk meg az x 4 + 1 2 x 3 - 5 2 x - 3 = 0 egyenlet valódi gyökereit.

Megoldás

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Az egyenlet mindkét oldalán megszorozzuk 2 3-mal:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Az y = 2 x változók cseréje:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 év 4 + y 3 - 20 év - 48 = 0

Ennek eredményeként egy 4. fokú standard egyenletet kaptunk, amely a standard séma szerint megoldható. Ellenőrizzük az osztókat, osszuk el, és végül kapjuk meg, hogy van 2 valós gyöke y = - 2, y = 3 és két összetett. Itt nem mutatjuk be a teljes megoldást. A behelyettesítés miatt ennek az egyenletnek a valódi gyöke x = y 2 = - 2 2 = - 1 és x = y 2 = 3 2 lesz.

Válasz: x 1 = - 1, x 2 = 3 2

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt

Látogasson el weboldalunk youtube csatornájára, hogy naprakész legyen az új videóleckékről.

Először is emlékezzünk a hatványok alapvető képleteire és tulajdonságaikra.

Egy szám szorzata a n-szer fordul elő önmagán, ezt a kifejezést a a … a=a n alakban írhatjuk fel

1. a 0 = 1 (a ≠ 0)

3. a n a m = a n + m

4. (a n) m = a nm

5. a n b n = (ab) n

7. a n / a m = a n - m

Teljesítmény ill exponenciális egyenletek – ezek olyan egyenletek, amelyekben a változók hatványban (vagy kitevőben) vannak, és az alap egy szám.

Példák exponenciális egyenletekre:

BAN BEN ebben a példában a 6-os az alap, mindig alul van, és a változó x fokozat vagy mutató.

Adjunk még példákat az exponenciális egyenletekre.
2 x *5=10
16 x - 4 x - 6 = 0

Most nézzük meg, hogyan oldják meg az exponenciális egyenleteket?

Vegyünk egy egyszerű egyenletet:

2 x = 2 3

Ezt a példát még fejben is meg lehet oldani. Látható, hogy x=3. Végül is, ahhoz, hogy a bal és a jobb oldal egyenlő legyen, x helyett 3-as számot kell tennie.
Most pedig nézzük meg, hogyan formálhatjuk ezt a döntést:

2 x = 2 3
x = 3

Egy ilyen egyenlet megoldása érdekében eltávolítottuk azonos indokok(vagyis kettesek) és felírta, ami maradt, ezek fokozatok. Megkaptuk a választ, amit kerestünk.

Most pedig foglaljuk össze döntésünket.

Algoritmus az exponenciális egyenlet megoldására:
1. Ellenőrizni kell ugyanaz hogy az egyenletnek van-e alapja a jobb és a bal oldalon. Ha az okok nem ugyanazok, akkor keressük a megoldási lehetőségeket ennek a példának a megoldására.
2. Miután az alapok azonosak lettek, egyenlővé tenni fokot, és oldja meg a kapott új egyenletet.

Most nézzünk néhány példát:

Kezdjük valami egyszerűvel.

A bal és a jobb oldalon lévő alapok egyenlőek a 2-es számmal, ami azt jelenti, hogy eldobhatjuk az alapot, és egyenlővé tehetjük a hatalmukat.

x+2=4 A legegyszerűbb egyenletet kapjuk.
x=4–2
x=2
Válasz: x=2

A következő példában láthatja, hogy az alapok különböznek: 3 és 9.

3 3x - 9 x+8 = 0

Először mozgassa a kilencet jobb oldalra, így kapjuk:

Most ugyanazokat az alapokat kell elkészítenie. Tudjuk, hogy 9=3 2. Használjuk az (a n) m = a nm hatványképletet.

3 3x = (3 2) x+8

9 x+8 =(3 2) x+8 =3 2x+16-ot kapunk

3 3x = 3 2x+16 Most már világos, hogy a bal és a jobb oldalon az alapok azonosak, és egyenlők hárommal, ami azt jelenti, hogy eldobhatjuk őket, és egyenlővé tesszük a fokokat.

3x=2x+16 a legegyszerűbb egyenletet kapjuk
3x - 2x=16
x=16
Válasz: x=16.

Nézzük a következő példát:

2 2x+4 - 10 4 x = 2 4

Először is nézzük meg az alapokat, a második és a negyedik alapot. És szükségünk van arra, hogy egyformák legyenek. A négyet az (a n) m = a nm képlettel alakítjuk át.

4 x = (2 2) x = 2 2x

És egy képletet is használunk a n a m = a n + m:

2 2x+4 = 2 2x 2 4

Adjuk hozzá az egyenlethez:

2 2x 2 4 - 10 2 2x = 24

Ugyanezen okokból adtunk egy példát. De a többi 10-es és 24-es szám zavar minket. Mit kezdjünk velük? Ha alaposan megnézed, láthatod, hogy a bal oldalon 2 2x ismétlődik, itt a válasz - 2 2x zárójelbe tehetünk:

2 2x (2 4 - 10) = 24

Számítsuk ki a zárójelben lévő kifejezést:

2 4 — 10 = 16 — 10 = 6

A teljes egyenletet elosztjuk 6-tal:

Képzeljük el, hogy 4=2 2:

2 2x = 2 2 bázis azonos, ezeket elvetjük és a fokokat egyenlővé tesszük.
2x = 2 a legegyszerűbb egyenlet. Oszd el 2-vel és megkapjuk
x = 1
Válasz: x = 1.

Oldjuk meg az egyenletet:

9 x – 12*3 x +27= 0

Alakítsuk át:
9 x = (3 2) x = 3 2x

Kapjuk az egyenletet:
3 2x - 12 3 x +27 = 0

Az alapjaink azonosak, egyenlők hárommal. Ebben a példában láthatjuk, hogy az első háromnak kétszer (2x) a foka, mint a másodiknak (csak x). Ebben az esetben meg tudod oldani cseremódszer. A számot a legkisebb fokozatra cseréljük:

Ekkor 3 2x = (3 x) 2 = t 2

Az egyenletben szereplő összes x hatványt t-re cseréljük:

t 2 - 12t+27 = 0
Másodfokú egyenletet kapunk. A diszkrimináns segítségével megoldva a következőket kapjuk:
D=144-108=36
t 1 = 9
t2 = 3

Visszatérve a változóhoz x.

Vegyük a t 1-et:
t 1 = 9 = 3 x

vagyis

3 x = 9
3 x = 3 2
x 1 = 2

Egy gyökér található. t 2-ből keressük a másodikat:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Válasz: x 1 = 2; x 2 = 1.

A honlapon a SEGÍTSÉG DÖNTÉS rovatában felteheti érdeklődését, mi biztosan válaszolunk.

Csatlakozz a csoporthoz