Transformimi i integralit të dyfishtë të koordinatave drejtkëndore,  te koordinatat polare
te koordinatat polare  , lidhur me koordinatat drejtkëndore nga relacionet
, lidhur me koordinatat drejtkëndore nga relacionet  ,
, , kryhet sipas formulës
, kryhet sipas formulës
Nëse fusha e integrimit  kufizuar në dy rreze
kufizuar në dy rreze  ,
, (
( ), duke dalë nga poli, dhe dy kthesa
), duke dalë nga poli, dhe dy kthesa  Dhe
Dhe  , atëherë integrali i dyfishtë llogaritet duke përdorur formulën
, atëherë integrali i dyfishtë llogaritet duke përdorur formulën
 .
.
Shembulli 1.3. Llogaritni sipërfaqen e figurës së kufizuar nga këto rreshta:  ,
, ,
, ,
, .
.
Zgjidhje. Për të llogaritur sipërfaqen e një zone  Le të përdorim formulën:
Le të përdorim formulën:  .
.
|
|
Le të përshkruajmë zonën ,
,
Le të kalojmë te koordinatat polare:
Në sistemin e koordinatave polar, zona |





 .
.
1.2. Integrale të trefishta
Vetitë themelore të integraleve të trefishta janë të ngjashme me vetitë e integraleve të dyfishta.
Në koordinatat karteziane, integrali i trefishtë zakonisht shkruhet si më poshtë:
 .
.
Nëse  , pastaj integrali i trefishtë mbi sipërfaqen
, pastaj integrali i trefishtë mbi sipërfaqen  numerikisht e barabartë me vëllimin e trupit
numerikisht e barabartë me vëllimin e trupit  :
:
 .
.
Llogaritja e trefishtë integrale
Lëreni fushën e integrimit  të kufizuara përkatësisht poshtë dhe sipër, me sipërfaqe të vazhdueshme me një vlerë të vetme
të kufizuara përkatësisht poshtë dhe sipër, me sipërfaqe të vazhdueshme me një vlerë të vetme  ,
, , dhe projeksioni i rajonit
, dhe projeksioni i rajonit  në planin koordinativ
në planin koordinativ  ka një zonë të sheshtë
ka një zonë të sheshtë  (Fig. 1.6).
(Fig. 1.6).
|
|
Pastaj për vlerat fikse Pastaj marrim:
Nëse përveç kësaj projeksioni
Ku |
 .
.
Shembulli 1.4. Llogaritni  , Ku
, Ku  - një trup i kufizuar nga avionë:
- një trup i kufizuar nga avionë:
|
|
Zgjidhje. Zona e integrimit është një piramidë (Fig. 1.7). Zona e projektimit
|
|
|
Vendosja e kufijve të integrimit për një trekëndësh
|
Integrali i trefishtë në koordinata cilindrike
Kur lëviz nga koordinatat karteziane  te koordinatat cilindrike
te koordinatat cilindrike  (Fig. 1.9) lidhur me
(Fig. 1.9) lidhur me  marrëdhëniet
marrëdhëniet  ,
, ,
, , dhe
, dhe
|
|
integrali i trefishtë transformohet: Shembulli 1.5. Llogaritni vëllimin e një trupi të kufizuar nga sipërfaqet: Zgjidhje. Vëllimi i kërkuar i trupit |
|
|
Fusha e integrimit është një pjesë e një cilindri të kufizuar më poshtë nga një plan Le të kalojmë te koordinatat cilindrike.
ose në koordinata cilindrike: |
Rajon  , i kufizuar nga një kurbë
, i kufizuar nga një kurbë  , do të marrë formën, ose
, do të marrë formën, ose  , ndërsa këndi polar
, ndërsa këndi polar
 . Si rezultat kemi
. Si rezultat kemi

 .
.
2. Elementet e teorisë së fushës
Le të kujtojmë fillimisht metodat për llogaritjen e integraleve lakor dhe sipërfaqësore.
Llogaritja e një integrali lakor mbi koordinatat e funksioneve të përcaktuara në një kurbë  , reduktohet në llogaritjen e një integrali të caktuar të formës
, reduktohet në llogaritjen e një integrali të caktuar të formës
nëse kurba  specifikuar në mënyrë parametrike
specifikuar në mënyrë parametrike  korrespondon me pikën e fillimit të kurbës
korrespondon me pikën e fillimit të kurbës  , A
, A  - pika e saj përfundimtare.
- pika e saj përfundimtare.
Llogaritja e integralit të sipërfaqes së një funksioni  , të përcaktuara në një sipërfaqe të dyanshme
, të përcaktuara në një sipërfaqe të dyanshme  , vjen deri te llogaritja e një integrali të dyfishtë, për shembull, të formës
, vjen deri te llogaritja e një integrali të dyfishtë, për shembull, të formës
|
|
nëse sipërfaqja  , dhënë nga ekuacioni
, dhënë nga ekuacioni  , është projektuar në mënyrë unike në aeroplan
, është projektuar në mënyrë unike në aeroplan  në rajon
në rajon  . Këtu
. Këtu  - këndi ndërmjet vektorit normal të njësisë
- këndi ndërmjet vektorit normal të njësisë  në sipërfaqe
në sipërfaqe  dhe boshti
dhe boshti  :
:
|
|
Ana e sipërfaqes e kërkuar nga kushtet e problemit  përcaktohet nga zgjedhja e shenjës së duhur në formulën (2.3).
përcaktohet nga zgjedhja e shenjës së duhur në formulën (2.3).
Përkufizimi 2.1. Fusha vektoriale
 quhet funksioni vektorial i një pike
quhet funksioni vektorial i një pike  së bashku me shtrirjen e tij:
së bashku me shtrirjen e tij:
Fusha vektoriale  karakterizohet nga një sasi skalare - divergjenca:
karakterizohet nga një sasi skalare - divergjenca:
Përkufizimi 2.2. Rrjedha
fushë vektoriale
 nëpër sipërfaqe
nëpër sipërfaqe
 quhet integral i sipërfaqes:
quhet integral i sipërfaqes:
|
|
Ku  - njësia e vektorit normal në anën e zgjedhur të sipërfaqes
- njësia e vektorit normal në anën e zgjedhur të sipërfaqes  , A
, A  - prodhim skalar i vektorëve
- prodhim skalar i vektorëve  Dhe
Dhe  .
.
Përkufizimi 2.3. Qarkullimi fushë vektoriale
Nga
kurba e mbyllur  quhet integral lakor
quhet integral lakor
|
|
Ku  .
.
Formula Ostrogradsky-Gauss
vendos një lidhje ndërmjet rrjedhës së fushës vektoriale
 përmes një sipërfaqe të mbyllur
përmes një sipërfaqe të mbyllur
 dhe divergjenca në terren:
dhe divergjenca në terren:
Ku
 - sipërfaqe e kufizuar nga një kontur i mbyllur
- sipërfaqe e kufizuar nga një kontur i mbyllur
 , A
, A
 është vektori normal njësi në këtë sipërfaqe. Drejtimi i normales duhet të jetë në përputhje me drejtimin e kalimit të konturit
është vektori normal njësi në këtë sipërfaqe. Drejtimi i normales duhet të jetë në përputhje me drejtimin e kalimit të konturit
 .
.
Shembulli 2.1. Llogaritni integralin e sipërfaqes
 ,
,
Ku  - pjesa e jashtme e konit
- pjesa e jashtme e konit  (
( ), i prerë nga një avion
), i prerë nga një avion  (Figura 2.1).
(Figura 2.1).
Zgjidhje. Sipërfaqe  projektuar në mënyrë unike në rajon
projektuar në mënyrë unike në rajon  aeroplan
aeroplan  , dhe integrali llogaritet duke përdorur formulën (2.2).
, dhe integrali llogaritet duke përdorur formulën (2.2).
|
|
Vektor normal i sipërfaqes së njësisë
Këtu, në shprehjen për normalen, zgjidhet shenja plus, që nga këndi |
Rajon  ka një rreth
ka një rreth  . Prandaj, në integralin e fundit kalojmë në koordinatat polare, ndërsa
. Prandaj, në integralin e fundit kalojmë në koordinatat polare, ndërsa  ,
, :
:
Shembulli 2.2. Gjeni divergjencën dhe përkuljen e një fushe vektoriale  .
.
Zgjidhje. Duke përdorur formulën (2.4) marrim
Rotori i një fushe të caktuar vektoriale gjendet duke përdorur formulën (2.5)

Shembulli 2.3. Gjeni fluksin e një fushe vektoriale  përmes një pjese të avionit
përmes një pjese të avionit  :
: , i vendosur në oktantin e parë (normalja formon një kënd akut me boshtin
, i vendosur në oktantin e parë (normalja formon një kënd akut me boshtin  ).
).
|
|
Zgjidhje. Në bazë të formulës (2.6)
Le të përshkruajmë një pjesë të aeroplanit
(Fig. 2.3). Vektori normal në aeroplan ka koordinata: |
|
|
|
Ku  - projeksion në plan
- projeksion në plan  në
në  (Fig. 2.4).
(Fig. 2.4).
Shembulli 2.4. Llogaritni fluksin e një fushe vektoriale nëpër një sipërfaqe të mbyllur  , i formuar nga avioni
, i formuar nga avioni  dhe një pjesë e konit
dhe një pjesë e konit  (
( ) (Fig. 2.2).
) (Fig. 2.2).
Zgjidhje. Le të përdorim formulën Ostrogradsky-Gauss (2.8)
 .
.
Le të gjejmë divergjencën e fushës vektoriale  sipas formulës (2.4):
sipas formulës (2.4):
Ku  është vëllimi i konit mbi të cilin kryhet integrimi. Le të përdorim formulën e njohur për të llogaritur vëllimin e një koni
është vëllimi i konit mbi të cilin kryhet integrimi. Le të përdorim formulën e njohur për të llogaritur vëllimin e një koni  (
( - rrezja e bazës së konit,
- rrezja e bazës së konit,  - e tij e lartë). Në rastin tonë ne marrim
- e tij e lartë). Në rastin tonë ne marrim  . Më në fund arrijmë
. Më në fund arrijmë
 .
.
Shembulli 2.5. Llogaritni qarkullimin e një fushe vektoriale  përgjatë konturit
përgjatë konturit
 , i formuar nga kryqëzimi i sipërfaqeve
, i formuar nga kryqëzimi i sipërfaqeve  Dhe
Dhe  (
( ). Kontrolloni rezultatin duke përdorur formulën Stokes.
). Kontrolloni rezultatin duke përdorur formulën Stokes.
Zgjidhje. Kryqëzimi i këtyre sipërfaqeve është një rreth  ,
, (Fig. 2.1). Drejtimi i kalimit zakonisht zgjidhet në mënyrë që zona e kufizuar prej saj të mbetet në të majtë. Le të shkruajmë ekuacionet parametrike të konturit
(Fig. 2.1). Drejtimi i kalimit zakonisht zgjidhet në mënyrë që zona e kufizuar prej saj të mbetet në të majtë. Le të shkruajmë ekuacionet parametrike të konturit
 :
:
|
|
dhe parametri  ndryshon nga
ndryshon nga  përpara
përpara  . Duke përdorur formulën (2.7), duke marrë parasysh (2.1) dhe (2.10), marrim
. Duke përdorur formulën (2.7), duke marrë parasysh (2.1) dhe (2.10), marrim
 .
.
Le të zbatojmë tani formulën e Stokes (2.9). Si sipërfaqe  , shtrirë në kontur
, shtrirë në kontur
 , ju mund të merrni një pjesë të avionit
, ju mund të merrni një pjesë të avionit  . Drejtim normal
. Drejtim normal  në këtë sipërfaqe është në përputhje me drejtimin e përshkimit të konturit
në këtë sipërfaqe është në përputhje me drejtimin e përshkimit të konturit
 . Rrotullimi i një fushe vektoriale të caktuar llogaritet në shembullin 2.2:
. Rrotullimi i një fushe vektoriale të caktuar llogaritet në shembullin 2.2:  . Prandaj, qarkullimi i dëshiruar
. Prandaj, qarkullimi i dëshiruar
Ku  - zona e rajonit
- zona e rajonit  .
. - rrezja e rrethit
- rrezja e rrethit  , ku
, ku
Le të kemi dy sisteme koordinative drejtkëndëshe në hapësirë dhe  , dhe një sistem funksionesh
, dhe një sistem funksionesh
 (1)
(1)
të cilat vendosin një korrespondencë një-për-një ndërmjet pikave në disa zona  Dhe
Dhe  në këto sisteme koordinative. Le të supozojmë se funksionet e sistemit (1) kanë
në këto sisteme koordinative. Le të supozojmë se funksionet e sistemit (1) kanë  derivatet e vazhdueshme të pjesshme. Përcaktori i përbërë nga këto derivate të pjesshme
derivatet e vazhdueshme të pjesshme. Përcaktori i përbërë nga këto derivate të pjesshme
 ,
,
quhet jakobiane (ose përcaktorja jakobiane) e sistemit të funksioneve (1). Ne do të supozojmë se  V
V  .
.
Sipas supozimeve të bëra më sipër, vlen formula e përgjithshme e mëposhtme për ndryshimin e variablave në një integral të trefishtë:

Ashtu si në rastin e integralit të dyfishtë, unike e ndërsjellë e sistemit (1) dhe kushtit  mund të shkelet në pika individuale, në vija individuale dhe në sipërfaqe të veçanta.
mund të shkelet në pika individuale, në vija individuale dhe në sipërfaqe të veçanta.
Sistemi i funksioneve (1) për çdo pikë  përputhet me një pikë të vetme
përputhet me një pikë të vetme  . Këta tre numra
. Këta tre numra  quhen koordinata kurvilineare të një pike
quhen koordinata kurvilineare të një pike  . Pikat e hapësirës
. Pikat e hapësirës  , për të cilat njëra nga këto koordinata ruan një vlerë konstante, formojnë të ashtuquajturat. sipërfaqe koordinative.
, për të cilat njëra nga këto koordinata ruan një vlerë konstante, formojnë të ashtuquajturat. sipërfaqe koordinative.
II Integrali i trefishtë në koordinata cilindrike
Sistemi cilindrik i koordinatave (CSS) përcaktohet nga rrafshi  , në të cilën specifikohet një sistem koordinativ polar dhe boshti
, në të cilën specifikohet një sistem koordinativ polar dhe boshti  , pingul me këtë rrafsh. Koordinatat cilindrike të një pike
, pingul me këtë rrafsh. Koordinatat cilindrike të një pike 
 , Ku
, Ku  – koordinatat polare të pikës
– koordinatat polare të pikës  – projeksionet t
– projeksionet t  syzet
syzet  tek avioni
tek avioni  , A
, A  – këto janë koordinatat e projeksionit të pikës
– këto janë koordinatat e projeksionit të pikës  për aks
për aks  ose
ose  .
.
Në aeroplan  ne futim koordinatat karteziane në mënyrën e zakonshme, drejtojmë boshtin e aplikuar përgjatë boshtit
ne futim koordinatat karteziane në mënyrën e zakonshme, drejtojmë boshtin e aplikuar përgjatë boshtit  CSK. Tani nuk është e vështirë të merren formula që lidhin koordinatat cilindrike me ato karteziane:
CSK. Tani nuk është e vështirë të merren formula që lidhin koordinatat cilindrike me ato karteziane:
 (3)
(3)
Këto formula hartojnë zonën në të gjithë hapësirën  .
.
Sipërfaqet e koordinatave në rastin në shqyrtim do të jenë:
1)
 – sipërfaqet cilindrike me gjenerata paralele me boshtin
– sipërfaqet cilindrike me gjenerata paralele me boshtin  , udhëzuesit e të cilit janë rrathë në aeroplan
, udhëzuesit e të cilit janë rrathë në aeroplan  , i përqendruar në pikë
, i përqendruar në pikë  ;
;
2)

 ;
;
3)
 – plane paralele me rrafshin
– plane paralele me rrafshin  .
.
Jacobian i sistemit (3):
 .
.
Formula e përgjithshme në rastin e CSK merr formën:
Shënim 1
.
Kalimi në koordinatat cilindrike rekomandohet në rastin kur zona e integrimit është një cilindër rrethor ose kon, ose një paraboloid i rrotullimit (ose pjesë të tij), dhe boshti i këtij trupi përkon me boshtin e aplikacionit.  .
.
Shënim 2. Koordinatat cilindrike mund të përgjithësohen në të njëjtën mënyrë si koordinatat polare në një plan.
Shembulli 1. Llogaritni integralin e trefishtë të një funksioni

sipas rajonit  , që përfaqëson pjesën e brendshme të cilindrit
, që përfaqëson pjesën e brendshme të cilindrit  , i kufizuar nga një kon
, i kufizuar nga një kon  dhe paraboloid
dhe paraboloid  .
.
Zgjidhje. Ne e kemi shqyrtuar tashmë këtë fushë në §2, shembulli 6, dhe kemi marrë një hyrje standarde në DPSC. Megjithatë, llogaritja e integralit në këtë rajon është e vështirë. Le të shkojmë në CSK:
 .
.
Projeksioni  trupi
trupi  tek avioni
tek avioni  - është një rreth
- është një rreth  . Prandaj, koordinata
. Prandaj, koordinata  varion nga 0 në
varion nga 0 në  , A
, A  - nga 0 në R.
Përmes një pike arbitrare
- nga 0 në R.
Përmes një pike arbitrare  vizatoni një vijë të drejtë paralele me boshtin
vizatoni një vijë të drejtë paralele me boshtin  . Vija e drejtë do të hyjë
. Vija e drejtë do të hyjë  në një kon, por do të dalë në një paraboloid. Por koni
në një kon, por do të dalë në një paraboloid. Por koni  ka ekuacionin në CSC
ka ekuacionin në CSC  , dhe paraboloidi
, dhe paraboloidi  - ekuacioni
- ekuacioni  . Pra kemi
. Pra kemi
III Integrali i trefishtë në koordinata sferike
Sistemi i koordinatave sferike (SCS) përcaktohet nga rrafshi  , në të cilën specifikohet UCS dhe boshti
, në të cilën specifikohet UCS dhe boshti  , pingul me rrafshin
, pingul me rrafshin  .
.
Koordinatat sferike të një pike  hapësira quhet trefishi i numrave
hapësira quhet trefishi i numrave  , Ku
, Ku  – këndi polar i projeksionit të një pike në një rrafsh
– këndi polar i projeksionit të një pike në një rrafsh  ,
, – këndi ndërmjet boshtit
– këndi ndërmjet boshtit  dhe vektor
dhe vektor  Dhe
Dhe  .
.
Në aeroplan  le të paraqesim boshtet e koordinatave karteziane
le të paraqesim boshtet e koordinatave karteziane  Dhe
Dhe  në mënyrën e zakonshme, dhe boshti aplikativ është i pajtueshëm me boshtin
në mënyrën e zakonshme, dhe boshti aplikativ është i pajtueshëm me boshtin  . Formulat që lidhin koordinatat sferike me ato karteziane janë si më poshtë:
. Formulat që lidhin koordinatat sferike me ato karteziane janë si më poshtë:
 (4)
(4)
Këto formula hartojnë zonën në të gjithë hapësirën  .
.
Jakobiani i sistemit të funksioneve (4):
 .
.
Ekzistojnë tre familje të sipërfaqeve koordinative:
1)
 – sfera koncentrike me qendër në origjinë;
– sfera koncentrike me qendër në origjinë;
2)
 – gjysmëplanet që kalojnë nëpër bosht
– gjysmëplanet që kalojnë nëpër bosht  ;
;
3)
 – kone rrethore me kulm në origjinë të koordinatave, boshti i të cilave është boshti
– kone rrethore me kulm në origjinë të koordinatave, boshti i të cilave është boshti  .
.
Formula për kalimin në SSC në integral të trefishtë:

Shënim 3.
Kalimi në SCS rekomandohet kur fusha e integrimit është një top ose pjesë e tij. Në këtë rast, ekuacioni i sferës  shkon në. Ashtu si CSK-ja e diskutuar më parë, CSK është "e lidhur" me boshtin
shkon në. Ashtu si CSK-ja e diskutuar më parë, CSK është "e lidhur" me boshtin  . Nëse qendra e sferës zhvendoset me një rreze përgjatë boshtit koordinativ, atëherë marrim ekuacionin sferik më të thjeshtë kur zhvendosemi përgjatë boshtit
. Nëse qendra e sferës zhvendoset me një rreze përgjatë boshtit koordinativ, atëherë marrim ekuacionin sferik më të thjeshtë kur zhvendosemi përgjatë boshtit  :
:
Shënim 4. Është e mundur të përgjithësohet SSC:

me Jacobian  . Ky sistem funksionesh do të përkthejë elipsoidin
. Ky sistem funksionesh do të përkthejë elipsoidin

në "paralelepiped"
Shembulli 2.
Gjeni distancën mesatare të pikave në një top me rreze  nga qendra e saj.
nga qendra e saj.
Zgjidhje.
Kujtojmë se vlera mesatare e funksionit  në zonë
në zonë  është integrali i trefishtë i një funksioni mbi një rajon të ndarë me vëllimin e rajonit. Në rastin tonë
është integrali i trefishtë i një funksioni mbi një rajon të ndarë me vëllimin e rajonit. Në rastin tonë
Pra kemi

Integrale të trefishta. Llogaritja e vëllimit të trupit.
Integrali i trefishtë në koordinata cilindrike
Për tre ditë i vdekuri shtrihej në zyrën e dekanit, i veshur me pantallonat e Pitagorës,
Në duart e Fichtenholtz-it ai mbante një vëllim që e kishte sjellë nga kjo botë,
Një integral i trefishtë ishte i lidhur në këmbë dhe kufoma ishte e mbështjellë në një matricë,
Dhe në vend që të lutej, një person i paturpshëm lexoi teoremën e Bernulit.
Integralet e trefishta janë diçka nga e cila nuk duhet të keni frikë =) Sepse nëse jeni duke e lexuar këtë tekst, atëherë, me shumë mundësi, ju keni një kuptim të mirë të teoria dhe praktika e integraleve “të zakonshëm”., dhe integrale të dyfishta. Dhe ku ka një dyshe, aty pranë ka një treshe:
![]()
Dhe me të vërtetë, çfarë ka për t'u frikësuar? Integrali është më pak, integrali është më shumë....
Le të shohim regjistrimin:
– ikonë integrale e trefishtë;
– integrand funksioni i tre variablave;
– produkt i diferencialeve.
- zona e integrimit.
Le të përqendrohemi veçanërisht në fushat e integrimit. Nëse në integral i dyfishtë ajo përfaqëson figurë e sheshtë, atëherë këtu - trup hapësinor, e cila, siç dihet, është e kufizuar nga grupi sipërfaqeve. Kështu, përveç sa më sipër, duhet të lundroni sipërfaqet bazë të hapësirës dhe të jetë në gjendje të bëjë vizatime të thjeshta tredimensionale.
Disa janë në depresion, e kuptoj... Mjerisht, artikulli nuk mund të titullohet "integrale të trefishta për dummies", dhe ka disa gjëra që duhet të dini/të jeni në gjendje t'i bëni. Por është në rregull - i gjithë materiali paraqitet në një formë jashtëzakonisht të arritshme dhe mund të zotërohet në kohën më të shkurtër të mundshme!
Çfarë do të thotë të llogaritësh një integral të trefishtë dhe çfarë është ai çift?
Për të llogaritur mesataren integrale të trefishtë gjeni NUMRIN:
Në rastin më të thjeshtë, kur integrali i trefishtë është numerikisht i barabartë me vëllimin e trupit. Dhe në të vërtetë, sipas kuptimi i përgjithshëm i integrimit, produkti është i barabartë pafundësisht i vogël vëllimi i një "tulle" elementare të trupit. Dhe integrali i trefishtë është vetëm bashkon
të gjitha këto grimca pafundësisht të vogla mbi sipërfaqen, duke rezultuar në vlerën integrale (të përgjithshme) të vëllimit të trupit: ![]() .
.
Për më tepër, integrali i trefishtë ka rëndësi aplikimet fizike. Por më shumë për këtë më vonë - në pjesën e dytë të mësimit, kushtuar llogaritjet e integraleve të trefishta arbitrare, për të cilin funksioni në rastin e përgjithshëm është i ndryshëm nga një konstante dhe është i vazhdueshëm në rajon. Në këtë artikull, ne do të shqyrtojmë në detaje problemin e gjetjes së vëllimit, i cili, sipas vlerësimit tim subjektiv, ndodh 6-7 herë më shpesh.
Si të zgjidhim një integral të trefishtë?
Përgjigja rrjedh logjikisht nga paragrafi i mëparshëm. Nevoja për të përcaktuar rendi i kalimit të trupit dhe shkoni në integrale të përsëritura. Pastaj trajtoni tre integrale të vetme në mënyrë sekuenciale.
Siç mund ta shihni, e gjithë kuzhina të kujton shumë, shumë integrale të dyfishta, me ndryshimin se tani kemi shtuar një dimension shtesë (përafërsisht, lartësia). Dhe, me siguri, shumë prej jush tashmë e kanë marrë me mend se si zgjidhen integralet e trefishta.
Le të shpërndajmë çdo dyshim të mbetur:
Shembulli 1
Ju lutemi shkruani në një kolonë në letër:
Dhe përgjigjuni pyetjeve të mëposhtme. A e dini se cilat sipërfaqe i përcaktojnë këto ekuacione? A e kuptoni kuptimin informal të këtyre ekuacioneve? A mund ta imagjinoni se si ndodhen këto sipërfaqe në hapësirë?
Nëse jeni të prirur për përgjigjen e përgjithshme "më tepër jo se po", atëherë sigurohuni që të punoni gjatë mësimit, përndryshe nuk do të përparoni më tej!
Zgjidhje: përdorim formulën.
Për të zbuluar rendi i kalimit të trupit dhe shkoni në integrale të përsëritura ju duhet (çdo gjë e zgjuar është e thjeshtë) për të kuptuar se çfarë lloj trupi është ky. Dhe në shumë raste, vizatimet kontribuojnë shumë në një kuptim të tillë.
Sipas kushteve, trupi kufizohet nga disa sipërfaqe. Ku të filloni ndërtimin? Unë sugjeroj procedurën e mëposhtme:
Së pari le të përshkruajmë paralele ortogonale projeksioni i trupit në rrafshin koordinativ. Hera e parë që thashë si quhet ky projeksion, lol =)
Meqenëse projeksioni kryhet përgjatë boshtit, atëherë para së gjithash këshillohet të merreni sipërfaqeve, të cilat janë paralele me këtë bosht. Më lejoni t'ju kujtoj se ekuacionet e sipërfaqeve të tilla mos përmbajnë shkronjën "z". Janë tre prej tyre në problemin në shqyrtim:
– ekuacioni specifikon një plan koordinativ që kalon nëpër bosht;
– ekuacioni specifikon një plan koordinativ që kalon nëpër bosht;
– grupet e ekuacionit aeroplan vijë e drejtë "e sheshtë". paralel me boshtin.
Me shumë mundësi, projeksioni i dëshiruar është trekëndëshi i mëposhtëm: 
Ndoshta jo të gjithë e kuptuan plotësisht për çfarë po flisnim. Imagjinoni që një bosht del nga ekrani i monitorit dhe ngjitet direkt në urën e hundës tuaj ( ato. rezulton se po shikoni një vizatim 3-dimensional nga lart). Trupi hapësinor në studim ndodhet në një "korridor" të pafund trekëndor dhe projeksioni i tij në një plan ka shumë të ngjarë të përfaqësojë një trekëndësh me hije.
Dëshiroj të tërheq vëmendje të veçantë për faktin se ndërkohë që jemi shprehur vetëm një supozim projeksioni dhe klauzolat "me shumë gjasa" dhe "me shumë gjasa" nuk ishin të rastësishme. Fakti është se jo të gjitha sipërfaqet janë analizuar ende dhe mund të ndodhë që njëra prej tyre të "presë" një pjesë të trekëndëshit. Si shembull i qartë, kjo sugjeron sferë me një qendër në origjinën e rrezes më të vogël se një, për shembull, një sferë ![]() – projeksioni i tij në aeroplan (rreth
– projeksioni i tij në aeroplan (rreth ![]() ) nuk do të "mbulojë" plotësisht zonën e hijezuar, dhe projeksioni përfundimtar i trupit nuk do të jetë fare një trekëndësh (rrethi do të "presë" qoshet e tij të mprehta).
) nuk do të "mbulojë" plotësisht zonën e hijezuar, dhe projeksioni përfundimtar i trupit nuk do të jetë fare një trekëndësh (rrethi do të "presë" qoshet e tij të mprehta).
Në fazën e dytë, ne zbulojmë se si trupi është i kufizuar nga lart dhe nga poshtë dhe kryejmë një vizatim hapësinor. Le të kthehemi te deklarata e problemit dhe të shohim se cilat sipërfaqe mbeten. Ekuacioni specifikon vetë planin koordinativ, dhe ekuacioni - cilindër parabolik, e vendosur sipër plan dhe duke kaluar nëpër bosht. Kështu, projeksioni i trupit është me të vërtetë një trekëndësh.
Meqë ra fjala, e gjeta këtu tepricë kushtet - nuk ishte e nevojshme të përfshihej ekuacioni i aeroplanit, pasi sipërfaqja, duke prekur boshtin e abshisës, tashmë e mbyll trupin. Është interesante të theksohet se në këtë rast nuk do të ishim në gjendje të vizatojmë menjëherë projeksionin - trekëndëshi do të "vizatohej" vetëm pasi të analizonim ekuacionin.
Le të përshkruajmë me kujdes një fragment të një cilindri parabolik: 
Pas përfundimit të vizatimeve me rendi i ecjes rreth trupit nuk ka problem!
Së pari, ne përcaktojmë rendin e kalimit të projeksionit (Në të njëjtën kohë, është SHUMË MË I KOSOVËS të lundrosh duke përdorur një vizatim dydimensional).Është bërë SAKTËSISË E NJËJTA, Si në integrale të dyfishta! Mendoni për një tregues lazer dhe për skanimin e një zone të sheshtë. Le të zgjedhim metodën e parë "tradicionale" të anashkalimit:
Tjetra, marrim një fanar magjik, shikojmë vizatimin tredimensional dhe rreptësisht nga poshtë lart Ne e ndriçojmë pacientin. Rrezet hyjnë në trup përmes një rrafshi dhe dalin përmes sipërfaqes. Kështu, rendi i kalimit të trupit është:
Le të kalojmë në integrale të përsëritura: 
1) Ju duhet të filloni me integralin "zeta". Ne përdorim Formula Njuton-Leibniz:
Le të zëvendësojmë rezultatin në integralin "lojë": 
Cfare ndodhi? Në thelb, zgjidhja u reduktua në një integral të dyfishtë, dhe pikërisht në formulë ![]() vëllimi i rrezes cilindrike! Ajo që vijon është e njohur:
vëllimi i rrezes cilindrike! Ajo që vijon është e njohur:
2) 
Kushtojini vëmendje teknikës racionale për zgjidhjen e integralit të 3-të.
Përgjigju: ![]()
Llogaritjet mund të shkruhen gjithmonë në "një rresht": 
Por kini kujdes me këtë metodë - fitimi në shpejtësi është i mbushur me humbje të cilësisë, dhe sa më kompleks të jetë shembulli, aq më i madh është shansi për të bërë një gabim.
Le t'i përgjigjemi një pyetjeje të rëndësishme:
A është e nevojshme të bëhen vizatime nëse kushtet e detyrës nuk kërkojnë zbatimin e tyre?
Ju mund të shkoni në katër mënyra:
1) Vizatoni projeksionin dhe vetë trupin. Ky është opsioni më i favorshëm - nëse keni mundësinë të përfundoni dy vizatime të mira, mos u bëni dembel, bëni të dy vizatimet. E rekomandoj fillimisht.
2) Vizatoni vetëm trupin. I përshtatshëm kur trupi ka një projeksion të thjeshtë dhe të dukshëm. Kështu, për shembull, në shembullin e çmontuar, do të mjaftonte një vizatim tredimensional. Sidoqoftë, ekziston edhe një minus - është e papërshtatshme të përcaktohet rradha e kalimit të projeksionit nga një foto 3D, dhe unë do ta rekomandoja këtë metodë vetëm për njerëzit me një nivel të mirë trajnimi.
3) Vizatoni vetëm projeksionin. Kjo gjithashtu nuk është e keqe, por më pas kërkohen komente shtesë me shkrim, që kufizon zonën nga anët e ndryshme. Fatkeqësisht, opsioni i tretë shpesh detyrohet - kur trupi është shumë i madh ose ndërtimi i tij është i mbushur me vështirësi të tjera. Dhe ne gjithashtu do të shqyrtojmë shembuj të tillë.
4) Bëni pa vizatime fare. Në këtë rast, duhet ta imagjinoni trupin mendërisht dhe të komentoni formën/vendndodhjen e tij me shkrim. I përshtatshëm për trupa ose detyra shumë të thjeshta ku kryerja e të dy vizatimeve është e vështirë. Por është akoma më mirë të bësh të paktën një vizatim skematik, pasi një zgjidhje "e zhveshur" mund të refuzohet.
Organi i mëposhtëm është për punë të pavarur:
Shembulli 2
Duke përdorur një integral të trefishtë, llogaritni vëllimin e një trupi të kufizuar nga sipërfaqet
Në këtë rast, fusha e integrimit specifikohet kryesisht nga pabarazitë, dhe kjo është edhe më mirë - një grup pabarazish ![]() përcakton oktantin e parë, duke përfshirë planet koordinative, dhe pabarazinë - gjysmë hapësirë, që përmban origjinën (kontrollo)+ vetë avioni. Plani "vertikal" pret paraboloidin përgjatë parabolës dhe këshillohet që ky seksion të ndërtohet në vizatim. Për ta bërë këtë, ju duhet të gjeni një pikë referimi shtesë, mënyra më e lehtë është kulmi i parabolës (Ne i konsiderojmë vlerat
përcakton oktantin e parë, duke përfshirë planet koordinative, dhe pabarazinë - gjysmë hapësirë, që përmban origjinën (kontrollo)+ vetë avioni. Plani "vertikal" pret paraboloidin përgjatë parabolës dhe këshillohet që ky seksion të ndërtohet në vizatim. Për ta bërë këtë, ju duhet të gjeni një pikë referimi shtesë, mënyra më e lehtë është kulmi i parabolës (Ne i konsiderojmë vlerat ![]() dhe llogaritni "zet" përkatës).
dhe llogaritni "zet" përkatës).
Le të vazhdojmë të ngrohemi:
Shembulli 3
Duke përdorur një integral të trefishtë, llogaritni vëllimin e trupit të kufizuar nga sipërfaqet e treguara. Ekzekutoni vizatimin.
Zgjidhje: Formulimi "ekzekutoni një vizatim" na jep njëfarë lirie, por ka shumë të ngjarë të nënkuptojë ekzekutimin e një vizatimi hapësinor. Sidoqoftë, as projeksioni nuk do të dëmtojë, veçanërisht pasi këtu nuk është më e thjeshta.
Ne i përmbahemi taktikave të provuara më parë - së pari do të merremi me të sipërfaqeve, të cilat janë paralele me boshtin aplikativ. Ekuacionet e sipërfaqeve të tilla nuk përmbajnë në mënyrë eksplicite variablin "z":
- ekuacioni specifikon planin koordinativ që kalon nëpër bosht ( e cila në aeroplan përcaktohet nga ekuacioni "eponim");
– grupet e ekuacionit aeroplan, duke kaluar përmes "eponimit" vijë e drejtë "e sheshtë". paralel me boshtin.
Trupi i dëshiruar kufizohet nga një aeroplan poshtë dhe cilindër parabolik lart: 
Le të krijojmë një rend të kalimit të trupit, ndërsa kufijtë "X" dhe "Y" të integrimit, ju kujtoj, është më i përshtatshëm për të gjetur duke përdorur një vizatim dydimensional:
Kështu: 
1) 
Kur integrohet mbi "y", "x" konsiderohet konstante, kështu që këshillohet që menjëherë të hiqet konstanta nga shenja integrale.
3) 
Përgjigju:
Po, pothuajse harrova, në shumicën e rasteve është pak e dobishme (dhe madje e dëmshme) të kontrollosh rezultatin e marrë me një vizatim tredimensional, pasi me një probabilitet të lartë iluzion vëllimi, për të cilën fola në klasë Vëllimi i një trupi revolucioni. Pra, duke vlerësuar trupin e problemit të konsideruar, mua personalisht më dukej se kishte shumë më tepër se 4 "kuba".
Shembulli i mëposhtëm për një zgjidhje të pavarur:
Shembulli 4
Duke përdorur një integral të trefishtë, llogaritni vëllimin e trupit të kufizuar nga sipërfaqet e treguara. Bëni vizatime të këtij trupi dhe projeksionit të tij në një plan.
Një shembull i përafërt i një detyre në fund të mësimit.
Nuk është e pazakontë kur ekzekutimi i një vizatimi tredimensional është i vështirë:
Shembulli 5
Duke përdorur një integral të trefishtë, gjeni vëllimin e një trupi të dhënë nga sipërfaqet e tij kufizuese
Zgjidhje: projeksioni këtu nuk është i komplikuar, por duhet të mendoni për rendin e kalimit të tij. Nëse zgjidhni metodën e parë, atëherë figura do të duhet të ndahet në 2 pjesë, gjë që kërcënon seriozisht për të llogaritur shumën dy integrale të trefishta. Në këtë drejtim, rruga e dytë duket shumë më premtuese. Le të shprehim dhe përshkruajmë projeksionin e këtij trupi në vizatim: 
Kërkoj ndjesë për cilësinë e disa prej fotove, i kam prerë direkt nga dorëshkrimet e mia.
Ne zgjedhim një renditje më të favorshme të kalimit të figurës: 
Tani i takon trupit. Nga poshtë kufizohet nga rrafshi, nga lart - nga rrafshi që kalon nëpër boshtin e ordinatave. Dhe gjithçka do të ishte mirë, por avioni i fundit është shumë i pjerrët dhe ndërtimi i zonës nuk është aq i lehtë. Zgjedhja këtu është e palakmueshme: ose punë bizhuteri në një shkallë të vogël (pasi trupi është mjaft i hollë), ose një vizatim rreth 20 centimetra i lartë (dhe madje edhe atëherë, nëse i përshtatet).
Por ekziston një metodë e tretë, vendase ruse për zgjidhjen e problemit - për të shënuar =) Dhe në vend të një vizatimi tredimensional, mjaftohuni me një përshkrim verbal: "Ky trup është i kufizuar nga cilindra ![]() dhe një aeroplan nga ana, një aeroplan nga poshtë dhe një aeroplan nga lart.”
dhe një aeroplan nga ana, një aeroplan nga poshtë dhe një aeroplan nga lart.”
Kufijtë "vertikalë" të integrimit janë padyshim:
Le të llogarisim vëllimin e trupit, duke mos harruar se ne e anashkaluam projeksionin në një mënyrë më pak të zakonshme: 
1) 
Përgjigju:
Siç e vutë re, trupat e propozuar në probleme që nuk janë më të shtrenjta se njëqind dollarë shpesh kufizohen nga rrafshi më poshtë. Por ky nuk është një rregull, kështu që gjithmonë duhet të jeni në roje - mund të hasni në një detyrë ku ndodhet trupi dhe nën banesë Kështu, për shembull, nëse në problemin e analizuar marrim parasysh rrafshin, atëherë trupi i ekzaminuar do të vendoset në mënyrë simetrike në gjysmëhapësirën e poshtme dhe do të kufizohet nga rrafshi nga poshtë dhe nga rrafshi nga lart!
Është e lehtë të shihet se ju merrni të njëjtin rezultat:
(Mos harroni se trupi duhet të ecë përreth rreptësisht nga poshtë lart!)
Për më tepër, avioni "i preferuar" mund të mos përdoret fare; shembulli më i thjeshtë: një top i vendosur mbi aeroplan - kur llogaritet vëllimi i tij, një ekuacion nuk do të nevojitet fare.
Ne do t'i shqyrtojmë të gjitha këto raste, por tani për tani ekziston një detyrë e ngjashme që ju ta zgjidhni vetë:
Shembulli 6
Duke përdorur integralin e trefishtë, gjeni vëllimin e një trupi të kufizuar nga sipërfaqet ![]()
Një zgjidhje dhe përgjigje e shkurtër në fund të mësimit.
Le të kalojmë në paragrafin e dytë me materiale po aq të njohura:
Integrali i trefishtë në koordinata cilindrike
Koordinatat cilindrike janë, në thelb, koordinatat polare në hapësirë.
Në një sistem koordinativ cilindrik, pozicioni i një pike në hapësirë përcaktohet nga koordinatat polare të pikës - projeksioni i pikës në plan dhe aplikimi i vetë pikës.
Kalimi nga një sistem kartezian tredimensional në një sistem koordinativ cilindrik kryhet sipas formulave të mëposhtme: 
Në lidhje me temën tonë, transformimi duket si ky:
Dhe, në përputhje me rrethanat, në rastin e thjeshtuar që po shqyrtojmë në këtë artikull: ![]()
Gjëja kryesore është të mos harroni për shumëzuesin shtesë "er" dhe ta vendosni saktë kufijtë polare të integrimit kur kaloni projeksionin:
Shembulli 7
Zgjidhje: i përmbahemi të njëjtës procedurë: para së gjithash, marrim parasysh ekuacionet në të cilat variabli “ze” mungon. Këtu është vetëm një. Projeksioni sipërfaqe cilindrike në aeroplan përfaqëson "eponimin" rrethi .
Aeroplanët ![]() ata kufizojnë trupin e dëshiruar nga poshtë dhe lart (e "prejnë" atë nga cilindri) dhe e projektojnë atë në një rreth:
ata kufizojnë trupin e dëshiruar nga poshtë dhe lart (e "prejnë" atë nga cilindri) dhe e projektojnë atë në një rreth: 
Më pas është një vizatim tredimensional. Vështirësia kryesore qëndron në ndërtimin e një rrafshi që kryqëzon cilindrin në një kënd "të zhdrejtë", duke rezultuar në elips. Le ta sqarojmë këtë pjesë në mënyrë analitike: për ta bërë këtë, ne rishkruajmë ekuacionin e planit në formë funksionale ![]() dhe llogaritni vlerat e funksionit ("lartësi") në pikat e dukshme që shtrihen në kufirin e projeksionit:
dhe llogaritni vlerat e funksionit ("lartësi") në pikat e dukshme që shtrihen në kufirin e projeksionit:

Pikat e gjetura i shënojmë në vizatim dhe me kujdes (jo si unë =)) lidhni ato me një linjë: 
Projeksioni i një trupi në një plan është një rreth, dhe ky është një argument i fortë në favor të lëvizjes në një sistem koordinativ cilindrik:
Le të gjejmë ekuacionet e sipërfaqeve në koordinata cilindrike:
Tani ju duhet të kuptoni rendin e kalimit të trupit.
Së pari, le të merremi me projeksionin. Si të përcaktohet rendi i kalimit të tij? SAKTËSISË TË NJËJTA SI ME llogaritja e integraleve të dyfishta në koordinata polare. Këtu është elementare:
Kufijtë "vertikalë" të integrimit janë gjithashtu të dukshëm - ne hyjmë në trup përmes aeroplanit dhe dalim nga ai përmes planit:
![]()
Le të kalojmë në integrale të përsëritura: 
Në këtë rast, ne vendosim menjëherë faktorin "er" në integralin "ton".
Si zakonisht, një fshesë është më e lehtë për t'u thyer përgjatë degëve:
1) 
Ne e vendosim rezultatin në integralin e mëposhtëm:
Dhe këtu nuk harrojmë se "phi" konsiderohet një konstante. Por kjo është për momentin:
Përgjigju:
Një detyrë e ngjashme për ju për të zgjidhur vetë:
Shembulli 8
Llogaritni vëllimin e një trupi të kufizuar nga sipërfaqet duke përdorur një integral të trefishtë. Vizatoni vizatimet e këtij trupi dhe projeksionin e tij në një rrafsh.
Një mostër e përafërt e modelit përfundimtar në fund të mësimit.
Ju lutemi vini re se në kushtet e problemeve nuk thuhet asnjë fjalë për kalimin në një sistem koordinativ cilindrik dhe një person injorant do të luftojë me integrale të vështira në koordinatat karteziane. ...Ose mbase nuk do - në fund të fundit, ekziston një mënyrë e tretë, origjinale ruse për zgjidhjen e problemeve =)
Është vetëm fillimi! ...në një mënyrë të mirë: =)
Shembulli 9
Duke përdorur integralin e trefishtë, gjeni vëllimin e një trupi të kufizuar nga sipërfaqet
Modeste dhe me shije.
Zgjidhje: ky organ është i kufizuar sipërfaqe konike Dhe paraboloid eliptik. Lexuesit që kanë lexuar me kujdes materialet e artikullit Sipërfaqet themelore të hapësirës, e kanë imagjinuar tashmë se si duket trupi, por në praktikë shpesh ka raste më komplekse, ndaj do të bëj një arsyetim të detajuar analitik.
Së pari, gjejmë linjat përgjatë të cilave kryqëzohen sipërfaqet. Le të hartojmë dhe zgjidhim sistemin e mëposhtëm:
Nga ekuacioni i parë zbresim termin e dytë me term:
Rezultati është dy rrënjë:
Le të zëvendësojmë vlerën e gjetur në çdo ekuacion të sistemit:
, nga ku rrjedh se
Kështu, rrënja korrespondon me një pikë të vetme - origjinën. Natyrisht, sepse kulmet e sipërfaqeve në shqyrtim përkojnë.
Tani le të zëvendësojmë rrënjën e dytë - gjithashtu në çdo ekuacion të sistemit:
Cili është kuptimi gjeometrik i rezultatit të marrë? "Në lartësi" (në rrafsh) paraboloidi dhe koni kryqëzohen së bashku rrethi– rrezja e njësisë me qendër në pikën .
Në këtë rast, "tasi" i paraboloidit përmban "gypin" e konit, pra duke formuar Sipërfaqja konike duhet të vizatohet me një vijë me pika (përveç segmentit të gjeneratorit më të largët nga ne, i cili është i dukshëm nga ky kënd):
Projeksioni i një trupi në një aeroplan është rrethi me një qendër në origjinën e rrezes 1, të cilën as që u mundova ta përshkruaj për shkak të qartësisë së këtij fakti (megjithatë, ne japim një koment me shkrim!). Meqë ra fjala, në dy problemet e mëparshme mund të shënohej edhe vizatimi i projeksionit, nëse jo për kushtin.
Kur kaloni në koordinatat cilindrike duke përdorur formula standarde, pabarazia shkruhet në formën e saj më të thjeshtë dhe nuk ka probleme me rendin e kalimit të projeksionit:
Le të gjejmë ekuacionet e sipërfaqeve në një sistem koordinativ cilindrik: ![]()
Meqenëse problemi merr në konsideratë pjesën e sipërme të konit, ne shprehemi nga ekuacioni:
"Ne skanojmë trupin" nga poshtë lart. Rrezet e dritës hyjnë në të përmes një paraboloidi eliptik dhe dalin përmes një sipërfaqe konike. Kështu, rendi "vertikal" i kalimit të trupit është:
Pjesa tjetër është çështje teknike: 
Përgjigju: ![]()
Nuk është e pazakontë që një trup të përcaktohet jo nga sipërfaqet e tij kufizuese, por nga shumë pabarazi:
Shembulli 10
![]()
Unë shpjegova kuptimin gjeometrik të pabarazive hapësinore në detaje të mjaftueshme në të njëjtin artikull referues - Sipërfaqet bazë të hapësirës dhe ndërtimi i tyre.
Edhe pse kjo detyrë përmban një parametër, ajo lejon ekzekutimin e një vizatimi të saktë që pasqyron pamjen bazë të trupit. Mendoni se si të ndërtoni. Një zgjidhje dhe përgjigje e shkurtër është në fund të mësimit.
...epo, disa detyra të tjera? Po mendoja të mbaroja mësimin, por thjesht ndjej se do më shumë =)
Shembulli 11
Duke përdorur një integral të trefishtë, llogaritni vëllimin e një trupi të caktuar: ![]() , ku është një numër pozitiv arbitrar.
, ku është një numër pozitiv arbitrar.
Zgjidhje: pabarazi ![]() përcakton një top me qendër në origjinën e rreze , dhe pabarazinë
përcakton një top me qendër në origjinën e rreze , dhe pabarazinë ![]() – “brenda” e një cilindri rrethor me një bosht simetrie të rrezes . Kështu, trupi i dëshiruar kufizohet nga një cilindër rrethor në anë dhe segmente sferike simetrike në lidhje me rrafshin në krye dhe në fund.
– “brenda” e një cilindri rrethor me një bosht simetrie të rrezes . Kështu, trupi i dëshiruar kufizohet nga një cilindër rrethor në anë dhe segmente sferike simetrike në lidhje me rrafshin në krye dhe në fund.
Duke e marrë këtë si njësinë bazë të matjes, le të vizatojmë: 
Më saktësisht, duhet të quhet vizatim, pasi nuk i mbajta shumë mirë përmasat përgjatë boshtit. Megjithatë, për të qenë të drejtë, kushti nuk kërkonte fare të vizatohej, dhe një ilustrim i tillë doli të ishte mjaft i mjaftueshëm.
Ju lutemi vini re se këtu nuk është e nevojshme të zbuloni lartësinë në të cilën cilindri shkurton "kapakët" nga topi - nëse merrni një busull në duar dhe e përdorni për të shënuar një rreth me një qendër në origjinën e rrezes 2 cm, atëherë pikat e kryqëzimit me cilindrin do të shfaqen vetë.
Integrali i trefishtë shkruhet si më poshtë:
Llogaritni integralin e trefishtë - nënkupton gjetjen e një numri të barabartë me vëllimin e trupit V ose, çfarë është e njëjta - zona V .
Pothuajse të gjithë mund ta kuptojnë kuptimin e llogaritjes së një integrali të trefishtë "mënyra e vështirë". Më saktësisht - "nën lëkurë", dhe akoma më saktë - në organet e tij të frymëmarrjes - mushkëritë. Pavarësisht nëse e dini apo jo, ka mbi 700 milionë alveola në mushkëritë e njeriut - formacione vezikulare të ndërthurura me një rrjet kapilarësh. Shkëmbimi i gazit ndodh përmes mureve të alveolave. Prandaj, mund të arsyetojmë kështu: vëllimi i gazit në mushkëri mund të përfaqësohet si një zonë kompakte. Dhe ky vëllim përbëhet nga vëllime të vogla të përqendruara në alveole. Rolin kryesor në këtë krahasim e luan numri i madh i alveolave në mushkëri: siç do të shohim në paragrafin tjetër, përmes një "numri të madh gjërash të vogla" koncepti i një integrali të trefishtë formulohet matematikisht.
Pse përdoret integrali i trefishtë për të gjetur vëllimin e një trupi? V? Lëreni zonën V ndarë në n zona arbitrare Δ vi, dhe ky përcaktim nënkupton jo vetëm çdo zonë të vogël, por edhe vëllimin e saj. Në secilën zonë kaq të vogël, zgjidhet një pikë arbitrare Mi, A f(Mi)- vlera e funksionit f(M) në këtë pikë. Tani do të maksimizojmë numrin e zonave të tilla të vogla dhe diametrin më të madh Δ vi- përkundrazi, zvogëloni. Mund të krijojmë një shumë integrale të formës
Nëse funksioni f(M) = f(x, y, z) është e vazhdueshme, do të ekzistojë kufiri i shumës integrale lloji i treguar më sipër. Ky kufi quhet integral i trefishtë .
Në këtë rast funksioni f(M) = f(x, y, z) quhet domain i integrueshëm V ; V- zona e integrimit; x, y, z- variablat e integrimit, dv(ose dx dy dz ) - element i vëllimit.
Llogaritja e integralit të trefishtë duke reduktuar shumësinë
Ashtu si në rastin e integraleve të dyfishta, llogaritja e integraleve të trefishta zvogëlohet në llogaritjen e integraleve me shumësi më të ulët.
Konsideroni një rajon tredimensional V. Poshtë dhe sipër (d.m.th., në lartësi) kjo zonë është e kufizuar nga sipërfaqet z = z1 (x, y) Dhe z = z2 (x, y) . Në anët (domethënë në gjerësi), zona është e kufizuar nga sipërfaqet y = y1 (x) Dhe y = y2 (x) . Dhe së fundi, në thellësi (nëse po shikoni zonën në drejtim të boshtit kau) - sipërfaqet x = a Dhe x = b
Për të aplikuar kalimin në integrale me shumësi më të ulët, kërkohet që domeni tredimensional V ishte e saktë. Është e saktë kur drejtëza është paralele me boshtin Oz, kalon kufirin e rajonit V në jo më shumë se dy pika. Rajonet e rregullta tre-dimensionale janë, për shembull, një kuboid, një elipsoid dhe një tetraedron. Në figurën e mëposhtme është paraqitur një paralelipiped drejtkëndor, të cilin do ta hasim në shembullin e parë të zgjidhjes së problemit.

Për të vizualizuar ndryshimin midis korrektësisë dhe pasaktësisë, shtojmë se sipërfaqet e rajonit përgjatë lartësisë së rajonit të saktë nuk duhet të jenë konkave nga brenda. Figura më poshtë është një shembull i një zone të pasaktë V- një hiperboloid me një fletë, sipërfaqja e të cilit është e drejtë, paralele me boshtin Oz(e kuqe), kryqëzohet në më shumë se dy pika.

Ne do të shqyrtojmë vetëm zonat e duhura.
Pra zona V- e saktë. Pastaj për çdo funksion f(x, y, z) , të vazhdueshme në rajon V, formula është e vlefshme

Kjo formulë ju lejon të zvogëloni llogaritjen e integralit të trefishtë në llogaritjen vijuese të integralit të brendshëm të caktuar mbi ndryshoren z(në konstante x Dhe y) dhe integrali i jashtëm i dyfishtë mbi një fushë dydimensionale D .
Duke kaluar nga integrali i dyfishtë në atë të përsëritur, marrim formulën e mëposhtme për llogaritjen e integralit të trefishtë:

Kështu, për të llogaritur një integral të trefishtë, duhet të vlerësoni në mënyrë sekuenciale tre integrale të përcaktuara.
Këto integrale llogariten nga pjesa më e brendshme (mbi ndryshoren z) në atë më të jashtmen (sipas ndryshores x). Për ta bërë më të lehtë për t'u kuptuar sekuencën e llogaritjeve, tre integrale "të mbivendosur" mund të shkruhen si më poshtë:
 .
.
Nga kjo hyrje tashmë është e qartë se:
- së pari ju duhet të integroni funksionin f(x, y, z) sipas ndryshores z, dhe merrni ekuacionet si kufijtë e integrimit z = z1 (x, y) Dhe z = z2 (x, y) sipërfaqet që kufizojnë zonën V poshtë dhe lart;
- y y = y1 (x) Dhe y = y2 (x) sipërfaqet që kufizojnë zonën V nga anët;
- integroni rezultatin e marrë në hapin e mëparshëm mbi variablin x, dhe merrni ekuacionet si kufijtë e integrimit x = a Dhe x = b sipërfaqet që kufizojnë zonën V në thellësi.
Shembulli 1. Le të kalojmë nga një integral i trefishtë në një integral të përsëritur
![]() -
-
sekuencat e tre integraleve të përcaktuara. Vlerësoni këtë integral të përsëritur.
Zgjidhje. Llogaritja e integralit të përsëritur gjithmonë fillon nga integrali i fundit:
![]() .
.
Le të llogarisim integralin e dytë - mbi ndryshoren y:
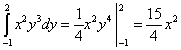 .
.
x:
 .
.
Përgjigje: Ky integral i përsëritur dhe integrali i trefishtë përkatës janë të barabartë me 10.
Shembulli 2. Llogaritni integralin e trefishtë
![]() ,
,
Ku V- paralelipiped i kufizuar nga plane x = − 1 , x = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .
Zgjidhje. Kufijtë e integrimit për të tre integralet e përcaktuara specifikohen në mënyrë unike nga ekuacionet e sipërfaqeve që kufizojnë paralelipipedin. Prandaj, ne e reduktojmë menjëherë këtë integral të trefishtë në një sekuencë prej tre integralesh të përcaktuara:
![]() .
.
z
 .
.
Ne llogarisim integralin "në mes" - mbi ndryshoren y. marrim;
![]() .
.
Tani ne llogarisim integralin më të jashtëm - mbi ndryshoren x:

Përgjigje: Ky integral i trefishtë është -2.
Shembulli 3. Llogaritni integralin e trefishtë
![]() ,
,
Ku Vx + y + z = 1 dhe aeroplanët koordinues x = 0 , y = 0 , z= 0. Rajon V projektuar në një aeroplan xOy në një trekëndësh D, siç tregohet në figurën më poshtë.

Zgjidhje. Le të vendosim së pari kufijtë e integrimit. Për integralin mbi një ndryshore z kufiri i poshtëm i integrimit specifikohet në mënyrë unike: z= 0. Për të marrë kufirin e sipërm, ne shprehim z nga x + y + z = 1 . Ne marrim 1 − x − y. Për integralin mbi një ndryshore y kufiri i poshtëm i integrimit specifikohet në mënyrë unike: y= 0. Për të marrë kufirin e sipërm, ne shprehim y nga x + y + z = 1 , duke pasur parasysh se z= 0 (pasi linja ndodhet në rrafsh xOy). Marrim: 1 − x .
Ne e zvogëlojmë këtë integral të trefishtë në një sekuencë prej tre integralesh të përcaktuara:
 .
.
Ne llogarisim integralin më të brendshëm - mbi një ndryshore z, duke marrë parasysh konstantet x dhe y. Ne marrim:
 .
.
y. Ne marrim:

x:

Përgjigje: Ky integral i trefishtë është i barabartë me 1/8.
Llogaritni vetë integralin e trefishtë dhe më pas shikoni zgjidhjen
Shembulli 4. Llogaritni integralin e trefishtë
![]() ,
,
Ku V- një piramidë e kufizuar nga një aeroplan x + y + z = 1 dhe aeroplanët koordinues x = 0 , y = 0 , z = 0 .
Rregullimi i kufijve të integrimit kur kalon në një sekuencë prej tre integralesh
Ndodh që studentët që nuk kanë ndonjë vështirësi të veçantë për të llogaritur drejtpërdrejt integralet, nuk mund të mësohen me vendosjen e kufijve të integrimit kur kalojnë nga një integral i trefishtë në një sekuencë prej tre integralesh të përcaktuar. Kjo çështje kërkon njëfarë trajnimi. Në shembullin e parë, fusha e integrimit V ishte një paralelipiped, me të cilin gjithçka është e qartë: kufizohet nga të gjitha anët me plane, që do të thotë se kufijtë e integrimit përcaktohen në mënyrë unike nga ekuacionet e planeve. Në shembullin e dytë - një piramidë: këtu ishte tashmë e nevojshme të mendohej pak më shumë dhe të shprehej një nga kufijtë nga ekuacioni. Dhe nëse zona V a janë të kufizuara nga sipërfaqet jo të sheshta? Sigurisht, është e nevojshme të inspektohet zona në një mënyrë të caktuar V .
Le të fillojmë me një shembull "më të tmerrshëm" për të ndjerë "situatën afër luftimit".
Shembulli 5. Rregulloni kufijtë e integrimit kur kaloni nga një integral i trefishtë, në të cilin rajoni V- elipsoid
![]() .
.

Zgjidhje. Le të jetë qendra e elipsoidit origjina, siç tregohet në figurën e mësipërme. Le të shohim elipsoidin nga poshtë. Kufizohet nga poshtë nga një sipërfaqe, e cila është ajo pjesë e sipërfaqes së elipsoidit që ndodhet poshtë rrafshit xOy z dhe shprehja që rezulton me shenjën minus do të jetë kufiri i poshtëm i integrimit mbi variablin z:
![]() .
.
Tani le të shohim elipsoidin nga lart. Këtu ai kufizohet nga një sipërfaqe, e cila është ajo pjesë e sipërfaqes së elipsoidit që ndodhet mbi bosht xOy. Prandaj, duhet të shprehemi nga ekuacioni elipsoid z dhe shprehja që rezulton do të jetë kufiri i sipërm i integrimit mbi variablin z:
![]() .
.
Projeksioni i një elipsoidi në një aeroplan xOyështë një elipsoid. Ekuacioni i tij:
Për të marrë kufirin e poshtëm të integrimit mbi një ndryshore y, duhet të shprehet y nga ekuacioni elipsoid dhe merrni shprehjen që rezulton me një shenjë minus:
![]() .
.
Për kufirin e sipërm të integrimit mbi një ndryshore y e njëjta shprehje me një shenjë plus:
Lidhur me integrimin mbi një ndryshore x, pastaj zona V e kufizuar në thellësi nga aeroplanët. Prandaj, kufijtë e integrimit mbi një ndryshore x mund të përfaqësohen si koordinatat e kufijve të pasmë dhe të përparmë të zonës. Në rastin e një elipsoidi, ato do të jenë vlerat e gjatësive gjysmë-boshtore të marra me shenja negative dhe pozitive. a: x1 = − a Dhe x2 = a .
Kështu, sekuenca e integraleve për llogaritjen e vëllimit të një elipsoidi është si më poshtë:
 ,
,
ku "yrek i pari", "yrek i dytë", "zet i pari" dhe "zet i dyti" janë shprehjet e marra më sipër. Nëse keni dëshirën dhe guximin për të llogaritur këtë integral dhe rrjedhimisht vëllimin e elipsoidit, atëherë ja ku është përgjigja: 4 πabc/3 .
Shembujt e mëposhtëm nuk janë aq të frikshëm sa ai që sapo u diskutua. Për më tepër, ato përfshijnë jo vetëm vendosjen e kufijve të integrimit, por edhe llogaritjen e vetë integralit të trefishtë. Provoni atë që keni mësuar duke ndjekur zgjidhjen e shembullit të frikshëm. Ju ende duhet të mendoni kur vendosni kufij.
Shembulli 6. Llogaritni integralin e trefishtë
nëse domeni i integrimit është i kufizuar me plane x + y = 1 , x + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .
Zgjidhje. Shembulli i “resortit” krahasohet me shembullin 5, pasi kufijtë e integrimit mbi “Y” dhe “Z” janë të përcaktuar në mënyrë unike. Por do të na duhet të merremi me kufijtë e integrimit mbi “X”. Projektimi i fushës së integrimit në plan xOyështë një trapez ABCD.

Në këtë shembull, është më e dobishme të projektohet trapezi në bosht Oy, përndryshe, për të llogaritur integralin e trefishtë, do të duhet ta ndani figurën në tre pjesë. Në shembullin 4 filluam të shqyrtojmë rajonin e integrimit nga poshtë, dhe kjo është procedura e zakonshme. Por në këtë shembull, ne e fillojmë inspektimin nga ana, ose, nëse është më e lehtë, vendosim figurën në anën e saj dhe konsiderojmë se po e shikojmë nga poshtë. Ne mund t'i gjejmë kufijtë e integrimit mbi "X" thjesht algjebrikisht. Për ta bërë këtë, ne shprehim "x" nga ekuacionet e para dhe të dyta të dhëna në kushtin e shembullit. Nga ekuacioni i parë fitojmë kufirin e poshtëm 1 − y, nga e dyta - e sipërme 4 − 2 y. Le ta reduktojmë këtë integral të trefishtë në një sekuencë prej tre integralesh të përcaktuara:
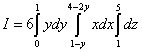 .
.
Kujdes! Në këtë shembull, integrali më i jashtëm nuk është mbi ndryshoren "x", por mbi ndryshoren "y", dhe integrali "mesatar" është mbi ndryshoren "x"! Këtu kemi aplikuar një ndryshim në rendin e integrimit, me të cilin jemi njohur gjatë studimit të integralit të dyfishtë. Kjo për faktin se, siç u përmend tashmë, ne filluam të shqyrtojmë rajonin e integrimit jo nga poshtë, por nga ana, domethënë, ne e projektuam atë jo në bosht. kau, për bosht Oy.
Ne llogarisim integralin më të brendshëm - mbi një ndryshore z, duke marrë parasysh konstantet x dhe y. Ne marrim:
Ne llogarisim integralin mesatar - mbi një ndryshore x. Ne marrim:
 .
.
Së fundi, ne llogarisim integralin më të jashtëm - mbi ndryshoren y:
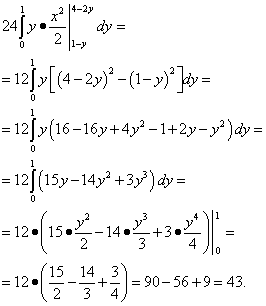
Përgjigje: Ky integral i trefishtë është i barabartë me 43.
Shembulli 7. Llogaritni integralin e trefishtë
![]() ,
,
nëse rajoni i integrimit është i kufizuar në sipërfaqe x = 0 , y = 0 , z = 2 , x + y + z = 4 .
Zgjidhje. Rajon V(piramida MNRP) eshte e sakte. Zona e projektimit V tek avioni xOyështë një trekëndësh AOB.

Kufijtë e poshtëm të integrimit për të gjitha variablat janë specifikuar në kushtin e shembullit. Le të gjejmë kufirin e sipërm të integrimit mbi "X". Për ta bërë këtë, ne shprehim "x" nga ekuacioni i katërt, duke konsideruar "y" të barabartë me zero dhe "ze" të barabartë me dy. marrim x= 2. Le të gjejmë kufirin e sipërm të integrimit mbi "lojën". Për ta bërë këtë, le të shprehim "Y" nga i njëjti ekuacion i katërt, duke e konsideruar "Z" të jetë e barabartë me dy dhe "X" të jetë një vlerë e ndryshueshme. marrim y = 2 − x. Dhe së fundi, ne gjejmë kufirin e sipërm të integrimit mbi ndryshoren "z". Për ta bërë këtë, le të shprehim "zet" nga i njëjti ekuacion i katërt, duke i konsideruar "y" dhe "zet" si sasi të ndryshueshme. marrim z = 4 − x − y .
Le ta reduktojmë këtë integral të trefishtë në një sekuencë prej tre integralesh të përcaktuara:
 .
.
Ne llogarisim integralin më të brendshëm - mbi një ndryshore z, duke marrë parasysh konstantet x dhe y. Ne marrim:
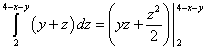 .
.
Ne llogarisim integralin mesatar - mbi një ndryshore y. Ne marrim:
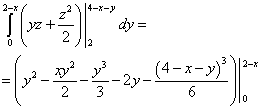 .
.
Ne llogarisim integralin më të jashtëm - mbi një ndryshore x dhe në fund gjejmë këtë integral të trefishtë:

Përgjigje: Ky integral i trefishtë është i barabartë me 2.
Ndryshimi i variablave në koordinatat e trefishta integrale dhe cilindrike
Nëse projeksioni i fushës së integrimit në cilindo plan koordinativ është një rreth ose pjesë e një rrethi, atëherë integrali i trefishtë është më i lehtë për t'u llogaritur duke kaluar në koordinatat cilindrike. Sistemi cilindrik i koordinatave është një përgjithësim sistemi i koordinatave polar në hapësirë. Në një sistem koordinativ cilindrik, një pikë M karakterizohet nga tre sasi ( r, φ , z), Ku r- distanca nga origjina në projeksion N pikë M tek avioni xOy, φ - këndi ndërmjet vektorit AKTIV dhe drejtimi i boshtit pozitiv kau, z- pika e aplikimit M(foto më poshtë).

Koordinatat drejtkëndore x, y, z me koordinata cilindrike r, φ , z lidh formulat
x = r cos φ ,
y = r mëkat φ ,
z = z .
Për të kaluar në koordinatat cilindrike në një integral të trefishtë, duhet të shprehni integrandin si funksion të ndryshoreve r, φ , z:
Kjo do të thotë, kalimi nga koordinatat drejtkëndore në cilindrike kryhet si më poshtë:
Integrali i trefishtë në koordinatat cilindrike llogaritet në të njëjtën mënyrë si në koordinatat drejtkëndore karteziane, duke e shndërruar atë në një sekuencë prej tre integralesh të përcaktuara:

Shembulli 8. Llogaritni integralin e trefishtë
![]()
kalimi në koordinatat cilindrike, ku V- zona e kufizuar nga sipërfaqet dhe.

Zgjidhje. Që nga zona V tek avioni xOy projektohet në një rreth, pastaj koordinata φ varion nga 0 në 2 π , dhe koordinata r- nga r=0 deri në r=1. Një vlerë konstante në hapësirë korrespondon me një cilindër. Duke marrë parasysh kryqëzimin e këtij cilindri me rajonin V, marrim një ndryshim në ordinate z nga z = r deri në z= 1. Le të kalojmë te koordinatat cilindrike dhe të marrim.
1. Koordinatat cilindrike paraqesin lidhjen e koordinatave polare në rrafshin xy me aplikimin e zakonshëm kartezian z (Fig. 3).
Le të jetë M(x, y, z) një pikë arbitrare në hapësirën xyz, P të jetë projeksioni i pikës M në rrafshin xy. Pika M përcaktohet në mënyrë unike nga një treshe numrash - koordinatat polare të pikës P, z - aplikojnë pikën M. Formulat që i lidhin me ato karteziane kanë formën
Harta Jakobiane (8)
Shembulli 2.
Llogarit integralin

ku T është sipërfaqja e kufizuar nga sipërfaqet

Zgjidhje. Le të kalojmë në koordinatat integrale në sferike duke përdorur formulat (9). Atëherë domeni i integrimit mund të specifikohet nga pabarazitë
Dhe kjo do të thotë

Shembulli 3 Gjeni vëllimin e trupit të kufizuar nga:
|
x 2 +y 2 +z 2 =8, |
Kemi: x 2 +y 2 +z 2 =8 - sferë me rreze R= v8 me qendër në pikën O(000),
Pjesa e sipërme e konit z 2 =x 2 +y 2 me bosht simetrie Oz dhe kulmin në pikën O (Fig. 2.20).
Le të gjejmë vijën e kryqëzimit të sferës dhe konit:

Dhe meqenëse sipas kushtit z? 0, atëherë

Rretho R=2 të shtrirë në rrafshin z=2.

Prandaj, sipas (2.28)

ku rajoni U kufizohet më sipër
(pjesë e sferës),
(pjesë e një koni);
rajoni U është projektuar në rrafshin Oxy në rajonin D - një rreth me rreze 2.
Prandaj, këshillohet të kaloni te koordinatat cilindrike në integralin e trefishtë duke përdorur formulat (2.36):
Kufijtë e ndryshimit q, r gjenden në zonën D v të rrethit të plotë R = 2 me qendër në pikën O, pra: 0? q? 2р, 0? r? 2. Kështu, rajoni U në koordinatat cilindrike jepet nga pabarazitë e mëposhtme:

vini re, se



Artikuj të ngjashëm


 (Fig. 1.5). Për ta bërë këtë, ne transformojmë kthesat:
(Fig. 1.5). Për ta bërë këtë, ne transformojmë kthesat: ,
, .
. ,
,
 .
. .
. përshkruar nga ekuacionet:
përshkruar nga ekuacionet:
 aplikimet përkatëse
aplikimet përkatëse  pikat e zonës
pikat e zonës  ndryshojnë brenda.
ndryshojnë brenda. .
. të përcaktuara nga pabarazitë
të përcaktuara nga pabarazitë ,
,
 ,
, - funksionet e vazhdueshme me një vlerë të vetme
- funksionet e vazhdueshme me një vlerë të vetme  , Kjo
, Kjo
 ,
,
 ,
, ,
, (
( ,
, ,
, ).
). ka një trekëndësh
ka një trekëndësh  , i kufizuar nga vija të drejta
, i kufizuar nga vija të drejta  ,
, ,
, (Fig. 1.8). Në
(Fig. 1.8). Në  dot aplikohet
dot aplikohet  kënaqin pabarazinë
kënaqin pabarazinë  , Kjo është arsyeja pse
, Kjo është arsyeja pse .
.
 , marrim
, marrim


 ,
,
 ,,
,, ,
, ,
, .
. barazohet
barazohet  .
.
 , dhe mbi aeroplan
, dhe mbi aeroplan  (Fig. 1.10). Zona e projektimit
(Fig. 1.10). Zona e projektimit  ka një rreth
ka një rreth  me qendër në origjinë dhe rreze njësi.
me qendër në origjinë dhe rreze njësi. ,
, ,
, . Në
. Në  dot aplikohet
dot aplikohet  , kënaqin pabarazinë
, kënaqin pabarazinë
 ,
, .
. ,
, ,
,
 gjejmë duke përdorur formulën (2.3):
gjejmë duke përdorur formulën (2.3): .
. ndërmjet boshtit
ndërmjet boshtit  dhe normale
dhe normale  - budalla dhe prandaj
- budalla dhe prandaj  duhet të jetë negativ. Duke marrë parasysh atë
duhet të jetë negativ. Duke marrë parasysh atë  , në një sipërfaqe
, në një sipërfaqe  marrim
marrim
 .
. :
: , i vendosur në oktantin e parë. Ekuacioni i këtij rrafshi në segmente ka formën
, i vendosur në oktantin e parë. Ekuacioni i këtij rrafshi në segmente ka formën
 , vektor normal njësi
, vektor normal njësi
 .
. .
. ,
,
 , ku
, ku  , prandaj,
, prandaj, ku
ku 



